
Next: Bibliography
Up: Proper elements for Earth
Previous: 7. Conclusions and future
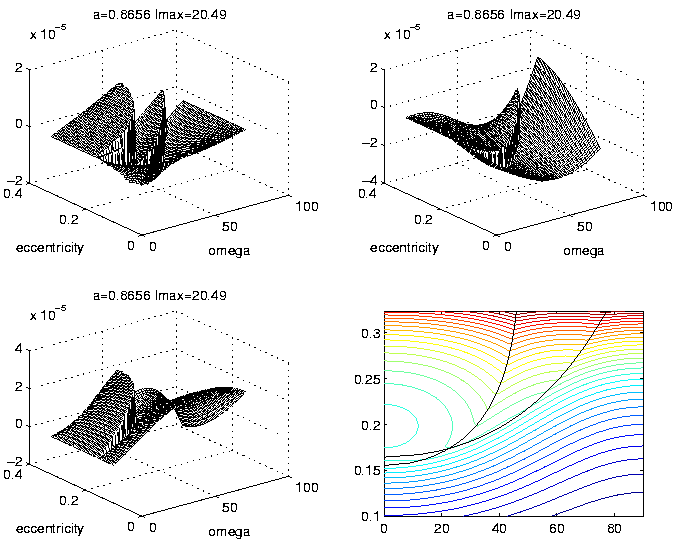
Figure:
An illustration of the discontinuity extraction
procedure. Top left: the graphic of the derivative of the integral
average of  with respect to
with respect to 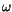 ,
as a function of
,
as a function of
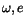 ;
there are two lines of discontinuity, corresponding to
crossings at the ascending node with the Earth and at the descending
one with Venus. Top right: the derivative of the integral average of
;
there are two lines of discontinuity, corresponding to
crossings at the ascending node with the Earth and at the descending
one with Venus. Top right: the derivative of the integral average of
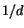 with respect to
with respect to 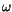 ;
note the discontinuity at the
ascending node with the Earth. Bottom left: the difference between the
two previous functions shows that the discontinuity due to the Earth
has been removed; note that the difference function is continuous, but
not differentiable along the ascending node crossing line. The
discontinuity at the descending node with Venus is still
present. Bottom right: the level curves of the integral average of
;
note the discontinuity at the
ascending node with the Earth. Bottom left: the difference between the
two previous functions shows that the discontinuity due to the Earth
has been removed; note that the difference function is continuous, but
not differentiable along the ascending node crossing line. The
discontinuity at the descending node with Venus is still
present. Bottom right: the level curves of the integral average of
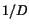 .
.
 |
This appendix contains the analytical formulas representing the
discontinuity of the derivatives of the averaged perturbing function
 .
.
If we choose, for instance, the direction from the
 to the
to the
 area, the difference in the twofold definition
of the derivatives of the averaged perturbing function are
area, the difference in the twofold definition
of the derivatives of the averaged perturbing function are
where
(see [Gronchi and Milani 1998] for the notation).
In case of crossing at the descending node, we have to modify the
previous formulas as follows:


Next: Bibliography
Up: Proper elements for Earth
Previous: 7. Conclusions and future
G.-F. Gronchi
2000-05-15


![]() .
.
![]() to the
to the
![]() area, the difference in the twofold definition
of the derivatives of the averaged perturbing function are
area, the difference in the twofold definition
of the derivatives of the averaged perturbing function are
![\begin{eqnarraystar}\mbox{Diff}\biggl({\partial\over \partial e}\vert d^+_{nod}\...
...mega}\biggr] =
-{2a(1-e^2)e\sin\omega\over(1+e\cos\omega)^2}
\end{eqnarraystar}](img163.gif)