Next: 4. DISCRETIZZAZIONE Up: 3. TEORIA QUALITATIVA Previous: 3.7 INSIEMI LIMITE Indice Indice analitico
Sommario Nel piano ![]() si possono caratterizzare tutti gli insiemi
si possono caratterizzare tutti gli insiemi
![]() -limite ed
-limite ed ![]() -limite, che o contengono punti di
equilibrio o sono cicli limite. Questo teorema non vale né su altre
varietà di dimensione 2 né in
-limite, che o contengono punti di
equilibrio o sono cicli limite. Questo teorema non vale né su altre
varietà di dimensione 2 né in ![]() per
per ![]() , dove la situazione
può essere molto più complicata.
, dove la situazione
può essere molto più complicata.
Ci limitiamo in questa sezione a considerare sistemi dinamici in
![]() . Sia
. Sia ![]() il campo vettoriale su un aperto
il campo vettoriale su un aperto
![]() che definisce il sistema dinamico, e prendiamo un qualunque punto
che definisce il sistema dinamico, e prendiamo un qualunque punto
![]() di
di ![]() che non sia un equilibrio, cioè tale che
che non sia un equilibrio, cioè tale che
![]() . Allora per
. Allora per ![]() passa una soluzione
passa una soluzione ![]() (con
(con
![]() ).
).
Definizione:
In altre parole, la sezione locale attraversa trasversalmente tutte le soluzioni del sistema dinamico che incontra.
In particolare una sezione locale non può passare per un punto di equilibrio.
Proprietà:
Se ![]() è l'immagine di una sezione locale, esiste un intorno
è l'immagine di una sezione locale, esiste un intorno ![]() di
di
![]() tale che tutte le soluzioni passanti dentro
tale che tutte le soluzioni passanti dentro ![]() devono
necessariamente incontrare anche
devono
necessariamente incontrare anche ![]() . Infatti la distanza da
. Infatti la distanza da ![]() (con
segno, tenendo conto dell'orientazione) ha derivata diversa da zero su
(con
segno, tenendo conto dell'orientazione) ha derivata diversa da zero su
![]() e (per continuità) su un suo intorno, e deve quindi passare dal
valore zero.
e (per continuità) su un suo intorno, e deve quindi passare dal
valore zero.
Una descrizione più precisa del comportamento delle soluzioni in un intorno di una sezione locale può essere ottenuta per mezzo del teorema di continuità del flusso, grazie al quale si può dare a tale intorno una struttura prodotto.
 |
La teoria qualitativa dei sistemi dinamici continui nel piano è resa
relativamente facile dal fatto che ci sono forti restrizioni, dovuti
alle proprietà topologiche del piano, alla maniera in cui una stessa
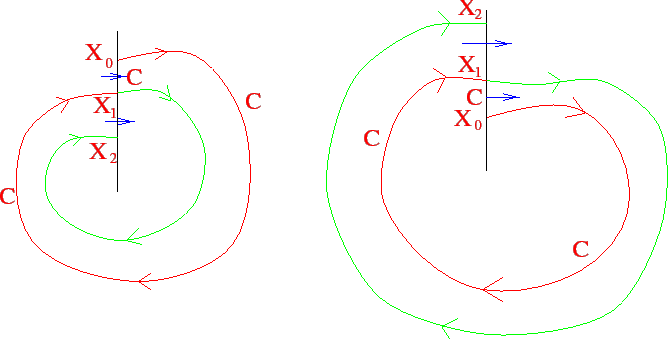
orbita può incontrare ripetutamente una sezione locale. Supponiamo
che ![]() sia una sezione locale in
sia una sezione locale in ![]() , con
, con ![]() , e che
, e che
![]() sia una soluzione tale che
sia una soluzione tale che ![]() ; per qualche
; per qualche ![]() sia
inoltre
sia
inoltre ![]() un punto che incontra la stessa sezione locale
un punto che incontra la stessa sezione locale
![]() , cioè esista un altro valore
, cioè esista un altro valore ![]() del parametro
del parametro ![]() tale
che
tale
che ![]() ; supponiamo infine
; supponiamo infine ![]() . Consideriamo allora la
figura formata dalla curva soluzione
. Consideriamo allora la
figura formata dalla curva soluzione ![]() per
per
![]() e
dalla sezione locale per
e
dalla sezione locale per
![]() : si tratta di una curva
chiusa
: si tratta di una curva
chiusa ![]() , differenziabile a tratti (vedi Figura 3.13).
, differenziabile a tratti (vedi Figura 3.13).
Si applica quindi il teorema della curva di Jordan, per
cui ![]() è diviso in due componenti connesse:
l'interno
è diviso in due componenti connesse:
l'interno ![]() , e l'esterno
, e l'esterno ![]() (rispetto alla curva
(rispetto alla curva
![]() ). Una qualsiasi curva continua non può uscire da
). Una qualsiasi curva continua non può uscire da ![]() senza
passare per
senza
passare per ![]() . In particolare una curva soluzione, come la curva
. In particolare una curva soluzione, come la curva
![]() stessa, una volta che si trovi dentro
stessa, una volta che si trovi dentro ![]() non può uscirne che
dal tratto
non può uscirne che
dal tratto ![]() della sezione locale. Però, la sezione essendo
trasversale, le soluzioni che passano da questo segmento o entrano
tutte o escono tutte da
della sezione locale. Però, la sezione essendo
trasversale, le soluzioni che passano da questo segmento o entrano
tutte o escono tutte da ![]() ; se la soluzione
; se la soluzione ![]() entra dentro
entra dentro ![]() ,
non può più uscirne per valori maggiori di
,
non può più uscirne per valori maggiori di ![]() ; se esce, non può
rientrare. Se ne deduce il lemma della sequenza monotona:
; se esce, non può
rientrare. Se ne deduce il lemma della sequenza monotona:
Lemma:
Dimostrazione del lemma:
L'arco di soluzione tra ![]() ed
ed ![]() , e l'arco di sezione
locale tra
, e l'arco di sezione
locale tra ![]() ed
ed ![]() formano una curva chiusa
formano una curva chiusa ![]() , per cui (come
illustrato dalla Figura 3.13) ci sono due soli casi: o la
soluzione non può più uscire dall'interno
, per cui (come
illustrato dalla Figura 3.13) ci sono due soli casi: o la
soluzione non può più uscire dall'interno ![]() di
di ![]() (Figura 3.13 a sinistra), e allora
(Figura 3.13 a sinistra), e allora ![]() sta in
sta in ![]() e
quindi `oltre'
e
quindi `oltre' ![]() lungo
lungo ![]() ; oppure la soluzione non può entrare
in
; oppure la soluzione non può entrare
in ![]() , e allora
, e allora ![]() si trova fuori da
si trova fuori da ![]() e quindi `oltre'
e quindi `oltre' ![]() lungo
lungo ![]() (Figura 3.13 a destra).
(Figura 3.13 a destra).
Il lemma precedente, ed il teorema di invarianza degli insiemi limite, consentono di dimostrare il risultato principale della teoria qualitativa dei sistemi dinamici nel piano.
Nel piano ![]() gli insiemi
gli insiemi ![]() -limite ed
-limite ed ![]() -limite
non vuoti e compatti, che non contengono
punti di equilibrio, sono orbite periodiche.
-limite
non vuoti e compatti, che non contengono
punti di equilibrio, sono orbite periodiche.
Dimostrazione (facoltativa):
L'orbita ![]() deve avere una successione di punti
deve avere una successione di punti ![]() con
con
![]() e
e ![]() , per definizione di
, per definizione di ![]() -limite;
ma allora a questa successione se ne può associare (almeno
definitivamente, per
-limite;
ma allora a questa successione se ne può associare (almeno
definitivamente, per ![]() abbastanza grande) un'altra
abbastanza grande) un'altra
![]() che appartiene alla sezione locale e che
tende a
che appartiene alla sezione locale e che
tende a ![]() lungo la sezione. Questo deriva dal fatto che la
successione
lungo la sezione. Questo deriva dal fatto che la
successione ![]() , avvicinandosi a
, avvicinandosi a ![]() , deve anche avvicinarsi
alla sezione locale, e quindi entrare nell'intorno di quest'ultima a
partire dal quale l'incontro con la sezione è inevitabile.
La successione
, deve anche avvicinarsi
alla sezione locale, e quindi entrare nell'intorno di quest'ultima a
partire dal quale l'incontro con la sezione è inevitabile.
La successione ![]() deve essere monotona sulla sezione locale
deve essere monotona sulla sezione locale ![]() ,
per il lemma della sequenza monotona, e tendere a
,
per il lemma della sequenza monotona, e tendere a
![]() .
.
Prendiamo uno di questi punti ![]() sulla sezione locale per
sulla sezione locale per ![]() :
poiché appartiene all'orbita per
:
poiché appartiene all'orbita per ![]() , è anche un punto
dell'
, è anche un punto
dell'![]() -limite di
-limite di ![]() (gli insiemi
(gli insiemi ![]() -limite sono
invarianti). Applicando lo stesso ragionamento, anche sull'orbita
-limite sono
invarianti). Applicando lo stesso ragionamento, anche sull'orbita
![]() si trova una successione di punti
si trova una successione di punti ![]() appartenenti
alla sezione locale
appartenenti
alla sezione locale ![]() , e che si avvicinano, al crescere di
, e che si avvicinano, al crescere di ![]() , in
modo monotono ad
, in
modo monotono ad ![]() .
.
Con da questa costruzione, si può completare la dimostrazione in quattro passi:
Passo 1: L'orbita per ![]() incontra la sezione locale
nel solo punto
incontra la sezione locale
nel solo punto ![]() . Se così non fosse, una seconda
intersezione
. Se così non fosse, una seconda
intersezione ![]() formerebbe con l'arco di orbita tra
formerebbe con l'arco di orbita tra ![]() e
e
![]() e l'arco di sezione tra
e l'arco di sezione tra ![]() e
e ![]() una curva chiusa
una curva chiusa ![]() ;
come nella Figura 3.13, si avrebbero due casi. Se
;
come nella Figura 3.13, si avrebbero due casi. Se ![]() sta rispetto ad
sta rispetto ad ![]() sulla sezione dalla parte opposta rispetto
agli
sulla sezione dalla parte opposta rispetto
agli ![]() , l'orbita contenente
, l'orbita contenente ![]() entra nell'interno
entra nell'interno ![]() di
di ![]() e non può più uscirne, mentre l'orbita
e non può più uscirne, mentre l'orbita ![]() non può
entrarvi. Ma allora vi sono dei punti sull'orbita per
non può
entrarvi. Ma allora vi sono dei punti sull'orbita per ![]() che non
possono essere punti limite dell'orbita
che non
possono essere punti limite dell'orbita ![]() . Se invece
. Se invece ![]() sta
rispetto ad
sta
rispetto ad ![]() sulla sezione dalla stessa parte degli
sulla sezione dalla stessa parte degli ![]() ,
i punti
,
i punti ![]() non possono avere
non possono avere ![]() come limite.
come limite.
Passo 2: L'orbita per ![]() incontra la stessa sezione
locale nel solo punto
incontra la stessa sezione
locale nel solo punto ![]() ; il ragionamento è identico a quello
del passo 1.
; il ragionamento è identico a quello
del passo 1.
Passo 3: L'orbita per ![]() , contenuta nell'insieme
, contenuta nell'insieme
![]() -limite dell'orbita
-limite dell'orbita ![]() , incontra la sezione locale nel
solo punto
, incontra la sezione locale nel
solo punto ![]() , mentre l'orbita stessa la incontra nel solo punto
, mentre l'orbita stessa la incontra nel solo punto
![]() . Questo è possibile solo se i due punti coincidono;
altrimenti ci sarebbe una distanza minima
. Questo è possibile solo se i due punti coincidono;
altrimenti ci sarebbe una distanza minima ![]() tra l'orbita
tra l'orbita ![]() e
e
![]() . Perciò
. Perciò ![]() è un'orbita periodica, perché
non può ripassare arbitrariamente vicino a
è un'orbita periodica, perché
non può ripassare arbitrariamente vicino a ![]() senza
passare dall'intorno della sezione locale a partire dal quale
l'incontro con la sezione è inevitabile, e quindi deve ripassare
esattamente dallo stesso punto.
senza
passare dall'intorno della sezione locale a partire dal quale
l'incontro con la sezione è inevitabile, e quindi deve ripassare
esattamente dallo stesso punto.
Passo 4: L'insieme limite di ![]() consiste solo della
traiettoria
consiste solo della
traiettoria ![]() dell'orbita periodica
dell'orbita periodica ![]() . Per il teorema della
curva di Jordan la traiettoria della soluzione
. Per il teorema della
curva di Jordan la traiettoria della soluzione ![]() deve stare tutta o nell'interno
deve stare tutta o nell'interno ![]() o nell'esterno
o nell'esterno ![]() della curva
della curva
![]() . Supponiamo che stia all'esterno: allora non può avere punti
limite all'interno, perché
. Supponiamo che stia all'esterno: allora non può avere punti
limite all'interno, perché ![]() è chiuso, ed i
valori limite di qualsiasi successione di punti di un chiuso devono
essere nel chiuso stesso. Perciò l'insieme limite
è chiuso, ed i
valori limite di qualsiasi successione di punti di un chiuso devono
essere nel chiuso stesso. Perciò l'insieme limite ![]() non contiene
punti di
non contiene
punti di ![]() . Se
. Se ![]() fosse un punto di
fosse un punto di ![]() , esiste un intorno
, esiste un intorno
![]() di
di ![]() che non contiene
che non contiene ![]() . L'orbita
. L'orbita ![]() ha infiniti punti
contenuti in
ha infiniti punti
contenuti in ![]() che tendono ad un punto
che tendono ad un punto ![]() di
di ![]() , in particolare
ve ne sono che stanno su di una sezione locale passante per
, in particolare
ve ne sono che stanno su di una sezione locale passante per ![]() . Per
il lemma della sequenza monotona, si costruisce come in
Figura 3.13 un insieme positivamente invariante che
contiene
. Per
il lemma della sequenza monotona, si costruisce come in
Figura 3.13 un insieme positivamente invariante che
contiene ![]() ma sta in
ma sta in ![]() , quindi non contiene
, quindi non contiene ![]() . Si ripete la
stessa costruzione del passo 1, e si mostra che l'orbita
. Si ripete la
stessa costruzione del passo 1, e si mostra che l'orbita ![]() non
può ripassare vicino a
non
può ripassare vicino a ![]() . Se invece
. Se invece ![]() sta all'interno, vale
lo stesso ragionamento scambiando il ruolo di
sta all'interno, vale
lo stesso ragionamento scambiando il ruolo di ![]() ed
ed ![]() .
.
Sia ![]() una curva chiusa che corrisponde ad una traiettoria di un
sistema dinamico in
una curva chiusa che corrisponde ad una traiettoria di un
sistema dinamico in ![]() , tale che l'insieme di definizione
, tale che l'insieme di definizione ![]() del
sistema dinamico contiene l'intera regione che sta
all'interno di
del
sistema dinamico contiene l'intera regione che sta
all'interno di ![]() . Allora all'interno di
. Allora all'interno di ![]() esiste o
almeno un punto di equilibrio o almeno un'altra orbita periodica
(distinta da
esiste o
almeno un punto di equilibrio o almeno un'altra orbita periodica
(distinta da ![]() ).
).
Dimostrazione:
Poiché per ipotesi ![]() , le soluzioni con condizioni
iniziali in
, le soluzioni con condizioni
iniziali in ![]() non possono uscire da
non possono uscire da ![]() , altrimenti dovrebbero
attraversare
, altrimenti dovrebbero
attraversare ![]() e questo contraddirebbe l'unicità della soluzione
per il punto di incrocio. D'altro canto
e questo contraddirebbe l'unicità della soluzione
per il punto di incrocio. D'altro canto ![]() è chiuso e
limitato, quindi compatto, e le soluzioni contenute in
è chiuso e
limitato, quindi compatto, e le soluzioni contenute in ![]() sono definite per ogni
sono definite per ogni ![]() in
in ![]() , per il teorema di
continuazione delle soluzioni. Perciò esse hanno insieme
, per il teorema di
continuazione delle soluzioni. Perciò esse hanno insieme
![]() -limite (anche
-limite (anche ![]() -limite) non vuoto. L'insieme
-limite) non vuoto. L'insieme
![]() -limite, oppure quello
-limite, oppure quello ![]() -limite, potrebbe essere
-limite, potrebbe essere ![]() (come in Figura 3.12); però
(come in Figura 3.12); però ![]() non può essere
contemporaneamente sia
non può essere
contemporaneamente sia ![]() -limite che
-limite che ![]() -limite, senza
contraddire il Lemma della sequenza monotona. Quindi, per il
teorema di Poincaré-Bendixon,
dentro
-limite, senza
contraddire il Lemma della sequenza monotona. Quindi, per il
teorema di Poincaré-Bendixon,
dentro ![]() deve esserci o un punto di equilibrio o un ciclo limite.
deve esserci o un punto di equilibrio o un ciclo limite.
Se però dentro ![]() esistesse un ciclo limite
esistesse un ciclo limite ![]() , questo
racchiuderebbe un insieme invariante
, questo
racchiuderebbe un insieme invariante ![]() , a cui si può applicare
lo stesso ragionamento. A partire da questo argomento si potrebbe
dimostrare che
, a cui si può applicare
lo stesso ragionamento. A partire da questo argomento si potrebbe
dimostrare che ![]() contiene in ogni caso un punto di equilibrio; per
la dimostrazione si veda [Hirsch-Smale 74].
contiene in ogni caso un punto di equilibrio; per
la dimostrazione si veda [Hirsch-Smale 74].
Problema
Sia dato un sistema dinamico ![]() sulla corona circolare
sulla corona circolare
![]() , con il campo vettoriale
, con il campo vettoriale ![]() che non si annulla dentro e
che non si annulla dentro e ![]() e sul bordo di
e sul bordo di ![]() punta
``dentro'' di
punta
``dentro'' di ![]() . Allora c'è almeno un'orbita periodica.
(Soluzione)
. Allora c'è almeno un'orbita periodica.
(Soluzione)
Esercizio
Sia ![]() l'insieme nel piano
l'insieme nel piano ![]() dei punti tali che
dei punti tali che
Il teorema di Poincaré-Bendixon non vale in dimensione
![]() . Anche in dimensione 2, ma su superfici diverse dal piano,
possono esistere insiemi limite che non contengono equilibri ma sono
molto diversi da orbite periodiche.
. Anche in dimensione 2, ma su superfici diverse dal piano,
possono esistere insiemi limite che non contengono equilibri ma sono
molto diversi da orbite periodiche.
Esempio:
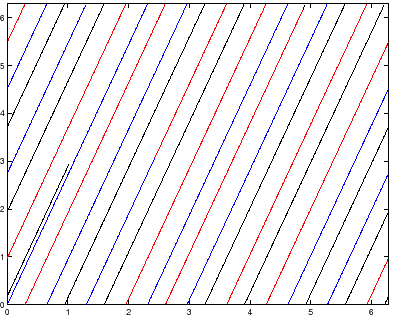 |
Come esempio di sistema dinamico continuo su ![]() prendiamo un
sistema dinamico costante su
prendiamo un
sistema dinamico costante su ![]() , cioè
, cioè
![]() e passiamolo al quoziente; si ottiene un sistema
dinamico sul toro, il cui flusso integrale va sotto il nome di
flusso di Kronecker. Se il rapporto
e passiamolo al quoziente; si ottiene un sistema
dinamico sul toro, il cui flusso integrale va sotto il nome di
flusso di Kronecker. Se il rapporto ![]() è
irrazionale, allora l'insieme
è
irrazionale, allora l'insieme ![]() -limite di ogni orbita è
tutto il toro; lo stesso per l'
-limite di ogni orbita è
tutto il toro; lo stesso per l'![]() -limite. Se invece
-limite. Se invece
![]() , tutte le orbite sono periodiche e quindi ciascuna
coincide con i propri insieme limite.
, tutte le orbite sono periodiche e quindi ciascuna
coincide con i propri insieme limite.
Andrea Milani 2009-06-01