Next: 5.2 INTEGRABILITÀ Up: 5. SISTEMI CONSERVATIVI Previous: 5. SISTEMI CONSERVATIVI Indice Indice analitico
Sommario I sistemi hamiltoniani generalizzano quelli newtoniani, e
sono caratterizzati dalla presenza di un integrale
primo. Perciò nel caso di un solo grado di libertà la descrizione
qualitativa delle soluzioni richiede soltanto lo studio di una
funzione di due variabili, come nel caso newtoniano. Inoltre
un sistema dinamico hamiltoniano è conservativo.
Consideriamo un
sistema newtoniano ad un grado di libertà
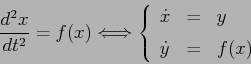
con energia potenziale, energia cinetica ed energia totale:
Le equazioni del sistema dinamico corrispondente possono essere
espresse in termini delle derivate dell'energia totale:
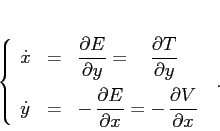
Questa forma delle equazioni si può generalizzare ad
una qualsiasi funzione di due variabili, detta
hamiltoniana ![]() : le
equazioni di Hamilton
definite da
: le
equazioni di Hamilton
definite da ![]() sono quelle
del sistema dinamico continuo
sono quelle
del sistema dinamico continuo
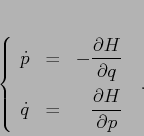
Ogni sistema dinamico che si può porre in questa forma si dice sistema hamiltoniano ad un grado di libertà.
Proprietà:
Infatti la derivata totale di ![]() è
è
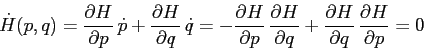
Se consideriamo il campo vettoriale gradiente ![]() definito dalla funzione hamiltoniana, esso è in ogni punto
perpendicolare al campo vettoriale che forma il secondo membro delle
equazioni di Hamilton. Le regole dei segni sono tali che il campo
vettoriale
definito dalla funzione hamiltoniana, esso è in ogni punto
perpendicolare al campo vettoriale che forma il secondo membro delle
equazioni di Hamilton. Le regole dei segni sono tali che il campo
vettoriale
![]() si ottiene dal gradiente
si ottiene dal gradiente ![]() mediante una rotazione di
mediante una rotazione di ![]() (in senso antiorario).
(in senso antiorario).
Un modo più sintetico di scrivere le equazioni di Hamilton fa uso
della matrice di tipo ![]() già utilizzata come unità
immaginaria nella rappresentazione matriciale dei numeri
complessi (nella Sezione 2.4):
già utilizzata come unità
immaginaria nella rappresentazione matriciale dei numeri
complessi (nella Sezione 2.4):
![\begin{displaymath}
\frac d{d\,t}\, \left[\begin{array}{c}{p}\\
{q}\end{array}...
...eft[\begin{array}{cc}{0}&{-1}\\
{1}&{0}\end{array}\right]\;,
\end{displaymath}](img1514.png)
per cui si può riscrivere la derivata totale di ![]() come
come
che si annulla perché una matrice antisimmetrica definisce una forma
quadratica nulla. Più in generale, data una qualunque funzione ![]() ,
la sua derivata totale si può descrivere con lo stesso metodo:
,
la sua derivata totale si può descrivere con lo stesso metodo:
dove il simbolo ![]() rappresenta la parentesi di Poisson che
ha la proprietà di antisimmetria
rappresenta la parentesi di Poisson che
ha la proprietà di antisimmetria
![]() , è lineare in
entrambi gli argomenti, e per tutte le funzioni
, è lineare in
entrambi gli argomenti, e per tutte le funzioni ![]() di classe
di classe
![]() soddisfa all'identità di Jacobi
soddisfa all'identità di Jacobi
![]() .
.
Esempio:
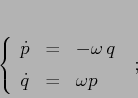
Il flusso integrale è dato dalle rotazioni di un angolo
![]() , cioè in verso positivo (antiorario) se
, cioè in verso positivo (antiorario) se ![]() .
.
Esempio:
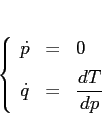
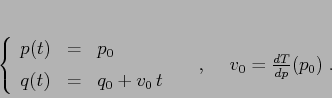
La hamiltoniana ![]() produce
produce
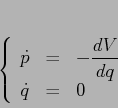
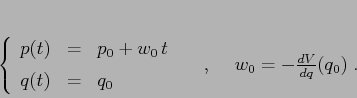
In entrambi i casi, il flusso integrale è costituito soltanto da scorrimenti.
I metodi simplettici a scorrimento, metodi di
integrazione numerica che approssimano un sistema hamiltoniano con
![]() mediante composizione di scorrimenti, in sostanza
alternano propagazioni della soluzione di
mediante composizione di scorrimenti, in sostanza
alternano propagazioni della soluzione di ![]() con
propagazioni della soluzione di
con
propagazioni della soluzione di ![]() .
.
Esempio:
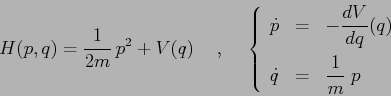
Poiché la funzione hamiltoniana è un integrale primo, lo studio
qualitativo del sistema dinamico è in sostanza lo stesso di quello
del sistema newtoniano ad un grado di libertà ![]() con
con
![]() , a parte il cambiamento di scala
, a parte il cambiamento di scala ![]() .
.
Strettamente parlando c'è un'altra differenza tra i due
sistemi dinamici: nel sistema dinamico
definito dalle equazioni di Hamilton la prima variabile è ![]() e la
seconda è
e la
seconda è ![]() , quindi c'è un cambiamento di orientazione, che
viene introdotto per ragioni di convenienza (per esempio, per far
ruotare le soluzioni dell'oscillatore armonico in verso positivo).
, quindi c'è un cambiamento di orientazione, che
viene introdotto per ragioni di convenienza (per esempio, per far
ruotare le soluzioni dell'oscillatore armonico in verso positivo).
Esempio:
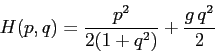
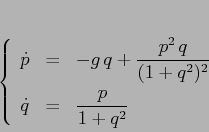
Questo esempio è un sistema hamiltoniano ma non un
sistema newtoniano, almeno non in queste coordinate. Come si vedrà
nella Sezione 5.4, questa hamiltoniana si può
ottenere dalla lagrangiana
di un moto vincolato
alla curva ![]() nel piano
nel piano ![]() .
.
La principale proprietà che contraddistingue i sistemi dinamici definiti da equazioni di Hamilton è che il relativo flusso integrale è conservativo:
Sia ![]() una funzione di classe
una funzione di classe ![]() . Se
. Se ![]() è la
soluzione con condizione iniziale
è la
soluzione con condizione iniziale ![]() , la trasformazione
, la trasformazione
conserva l'area, e questo per ogni ![]() per cui è definita.
Dimostrazione:
per cui è definita.
Dimostrazione:
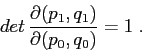
Usiamo gli sviluppi di Taylor delle soluzioni
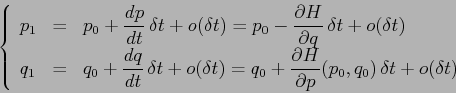
![\begin{displaymath}
det\,\frac{\partial {(p_1,q_1)}}{\partial {(p_0,q_0)}}
= ...
... {p}\,\partial{q}}(q_0,p_0)}\end{array}\right] + o(\delta t)
\end{displaymath}](img1549.png)
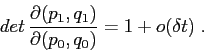
Descriviamo la propagazione dal tempo ![]() al tempo
al tempo ![]() come il
risultato di una sequenza di
come il
risultato di una sequenza di ![]() propagazioni per intervalli di tempo
uguali a
propagazioni per intervalli di tempo
uguali a ![]() . La matrice jacobiana della propagazione da
. La matrice jacobiana della propagazione da
![]() a
a ![]() è il prodotto di
è il prodotto di ![]() jacobiane. Quindi il determinante
jacobiano del loro prodotto è il prodotto di
jacobiane. Quindi il determinante
jacobiano del loro prodotto è il prodotto di ![]() jacobiani, ciascuno
della forma
jacobiani, ciascuno
della forma ![]() , e perciò vale
, e perciò vale ![]() . Il limite
per
. Il limite
per ![]() di questo prodotto di jacobiani è
di questo prodotto di jacobiani è ![]() . Questo
prodotto però è lo jacobiano del propagatore da
. Questo
prodotto però è lo jacobiano del propagatore da ![]() ad
ad ![]() , che
è un numero indipendente da
, che
è un numero indipendente da ![]() , quindi per avere limite 1 deve
essere esattamente
, quindi per avere limite 1 deve
essere esattamente ![]() .
.
Andrea Milani 2009-06-01