Next: A. REQUISITI DI ALGEBRA, Up: 6. CAOS Previous: 6.4 REGIONI ORDINATE Indice Indice analitico
Sommario Diverse definizioni di caos sono state proposte,
e ciascuna ha i suoi meriti; per esempio quella basata sugli esponenti
di Lyapounov. Nessuna però sembra capace sia di descrivere in modo
rigoroso alcune caratteristiche fondamentali del moto caotico, sia
dare luogo a risultati che consentano di descrivere esplicitamente
ampie regioni caotiche. Trovare una definizione di caos pienamente
soddisfacente resta quindi un problema aperto.
Dato un sistema dinamico discreto ![]() su
su ![]() (oppure
(oppure ![]() ), data
una condizione iniziale
), data
una condizione iniziale ![]() , e la sua orbita
, e la sua orbita
![]() , possiamo considerare il
linearizzato di
, possiamo considerare il
linearizzato di ![]() dato dalla
matrice
dato dalla
matrice ![]() e il linearizzato di ciascuna iterazione della
mappa:
e il linearizzato di ciascuna iterazione della
mappa:
Per generalizzare la definizione di esponente di Lyapounov ad un'orbita qualsiasi, non necessariamente periodica, si procede come segue.
Definizione:
Un esponente di Lyapounov misura il carattere esponenziale della
divergenza di orbite con condizioni iniziali vicine (in effetti,
infinitamente vicine, nel senso che si usano le derivate parziali
contenute nelle matrici jacobiane, non degli incrementi finiti). Il
vettore variazione cresce di lunghezza come
![]() ; ovvero,
; ovvero,
![]() è il tempo di Lyapounov in cui la lunghezza tende ad
aumentare di un fattore
è il tempo di Lyapounov in cui la lunghezza tende ad
aumentare di un fattore ![]() .
Non è detto che il limite per
.
Non è detto che il limite per ![]() esista;
perciò non per tutte le mappe
esista;
perciò non per tutte le mappe ![]() , e per tutte le condizioni
iniziali
, e per tutte le condizioni
iniziali ![]() , esistono gli esponenti di Lyapounov. Tuttavia nel caso
che lo spazio su cui si opera sia compatto, come è il caso
di
, esistono gli esponenti di Lyapounov. Tuttavia nel caso
che lo spazio su cui si opera sia compatto, come è il caso
di ![]() , gli esponenti di Lyapounov esisteranno per la maggior parte
delle condizioni iniziali.
, gli esponenti di Lyapounov esisteranno per la maggior parte
delle condizioni iniziali.
Esempio:
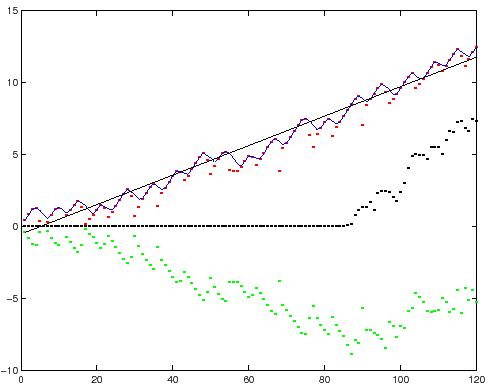 |
Scegliamo ora una condizione iniziale vicina, appartenente alla
regione caotica che circonda il punto fisso iperbolico: per esempio
con
![]() si ottengono i risultati della
Figura 6.15. Le curve tracciate per punti in figura
rappresentano, in funzione del numero di iterazioni
si ottengono i risultati della
Figura 6.15. Le curve tracciate per punti in figura
rappresentano, in funzione del numero di iterazioni ![]() : l'autovalore
maggiore di 1 di
: l'autovalore
maggiore di 1 di ![]() , il determinante di
, il determinante di ![]() , l'autovalore
minore di 1 di
, l'autovalore
minore di 1 di ![]() . Il determinante cessa di essere 1 per
effetto di arrotondamento; per esempio la matrice
. Il determinante cessa di essere 1 per
effetto di arrotondamento; per esempio la matrice ![]() ha
coefficienti dell'ordine di
ha
coefficienti dell'ordine di ![]() , quindi per calcolare il
determinante si fa la differenza di due numeri dell'ordine di
, quindi per calcolare il
determinante si fa la differenza di due numeri dell'ordine di
![]() , il che porta ad un valore calcolato del determinante
, il che porta ad un valore calcolato del determinante
![]() per effetto dell'errore di arrotondamento (la precisione
relativa dei calcoli, nella maggior parte dei calcolatori, non è
meglio di
per effetto dell'errore di arrotondamento (la precisione
relativa dei calcoli, nella maggior parte dei calcolatori, non è
meglio di ![]() ). Di conseguenza l'autovalore
minore di 1 non può più essere calcolata in modo attendibile per
). Di conseguenza l'autovalore
minore di 1 non può più essere calcolata in modo attendibile per
![]() , mentre l'autovalore maggiore è calcolato in modo
numericamente stabile. Le curve continue rappresentano
, mentre l'autovalore maggiore è calcolato in modo
numericamente stabile. Le curve continue rappresentano
![]() , dove
, dove ![]() è un vettore scelto a caso, e la
retta di regressione che approssima
è un vettore scelto a caso, e la
retta di regressione che approssima ![]() nel senso dei minimi
quadrati, dalla cui pendenza si ottiene una stima dell'esponente di
Lyapounov positivo:
nel senso dei minimi
quadrati, dalla cui pendenza si ottiene una stima dell'esponente di
Lyapounov positivo:
![]() .
.
 |
Esempio:
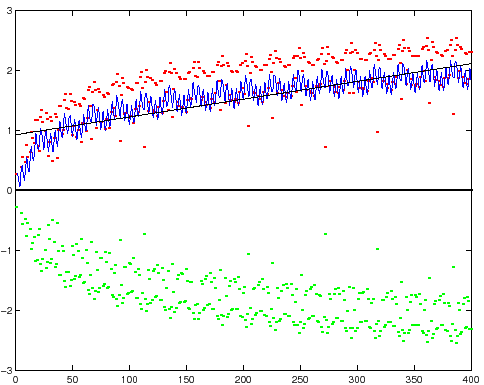
Ripetiamo l'esperimento numerico con una condizione iniziale nella
regione ordinata attorno al punto fisso ellittico: per
esempio con condizioni iniziali ![]() anche dopo
anche dopo ![]() iterazioni la lunghezza del vettore variazione non è aumentata di
molto; la retta di regressione suggerirebbe un esponente di Lyapounov
iterazioni la lunghezza del vettore variazione non è aumentata di
molto; la retta di regressione suggerirebbe un esponente di Lyapounov
![]() , ma dalla Figura 6.16 si penserebbe
piuttosto che la curva
, ma dalla Figura 6.16 si penserebbe
piuttosto che la curva ![]() possa avere un asintoto orizzontale.
possa avere un asintoto orizzontale.
Un programma Matlab per calcolare approssimazioni finite agli esponenti di Lyapounov: lyapexp.m
I due esempi qui sopra suggeriscono che si potrebbe cercare di caratterizzare le regioni caotiche ed ordinate in base ai valori degli esponenti di Lyapounov.
Definizione:
Questa definizione è relativamente semplice da enunciare, e si basa
su di una caratteristica importante, l'impossibilità di prevedere
l'orbita su tempi molto più lunghi del tempo di Lyapounov
![]() . Infatti per iterazioni con
. Infatti per iterazioni con ![]() ogni differenza di
condizioni iniziali viene amplificata di un fattore
ogni differenza di
condizioni iniziali viene amplificata di un fattore ![]() , e
anche soltanto l'arrotondamento inevitabile nei calcoli digitali
produce orbite del tutto diverse da quella esatta. Ancora peggio, se
il sistema dinamico corrisponde ad un sistema fisico le cui
proprietà sono misurate, le condizioni iniziali sono note con una
certa approssimazione, che si accresce con le iterazioni fino ad
impedire qualsiasi previsione al di là di un
orizzonte di prevedibilità.
, e
anche soltanto l'arrotondamento inevitabile nei calcoli digitali
produce orbite del tutto diverse da quella esatta. Ancora peggio, se
il sistema dinamico corrisponde ad un sistema fisico le cui
proprietà sono misurate, le condizioni iniziali sono note con una
certa approssimazione, che si accresce con le iterazioni fino ad
impedire qualsiasi previsione al di là di un
orizzonte di prevedibilità.
Gli inconvenienti principali sono due. Prima di tutto l'esponente di
Lyapounov è un limite per ![]() , se si vuol fare
riferimento alle Figure 6.15 e 6.16 è
proporzionale alla pendenza dell'asintoto, quindi una stima basata su
di un numero finito di iterazioni non consente di giungere ad alcuna
conclusione rigorosa. Perciò la facilità di calcolo degli
esponenti di Lyapounov è solo apparente, e la definizione di caos
basata su di essi non è verificabile con un numero finito di
operazioni.
, se si vuol fare
riferimento alle Figure 6.15 e 6.16 è
proporzionale alla pendenza dell'asintoto, quindi una stima basata su
di un numero finito di iterazioni non consente di giungere ad alcuna
conclusione rigorosa. Perciò la facilità di calcolo degli
esponenti di Lyapounov è solo apparente, e la definizione di caos
basata su di essi non è verificabile con un numero finito di
operazioni.
Secondo, abbiamo visto già dagli esempi che non è detto che una ``regione caotica'' che ci appare a prima vista come omogenea abbia lo stesso esponente di Lyapounov (positivo) dappertutto. Un aperto nello spazio delle condizioni iniziali può contenere una mistura di orbite tutte caotiche, ma in misura assai diversa, e magari con comportamenti qualitativamente diversi.
Un esempio di questi comportamenti diversi è dato dal fenomeno del ``caos stabile''. In poche parole, un'orbita può essere caotica (nel senso dell'esponente di Lyapounov positivo) e malgrado ciò comportarsi, per un tempo molto più lungo del tempo di Lyapounov, come un orbita stabile [Milani-Nobili 92].
Una possibile definizione alternativa di caos si basa sul teorema del punto omoclinico trasversale, e consiste nel richiedere un comportamento descrivibile in termini di dinamica simbolica.
Definizione:
Un'orbita del sistema dinamico discreto ![]() presenta il fenomeno del
caos se appartiene ad un insieme compatto
presenta il fenomeno del
caos se appartiene ad un insieme compatto ![]() ,
che è un insieme iperbolico per un'iterata
,
che è un insieme iperbolico per un'iterata ![]() di
di ![]() e
tale che la mappa
e
tale che la mappa ![]() ristretta a
ristretta a ![]() è coniugata
mediante un omeomorfismo ad uno scorrimento di Bernoulli.
è coniugata
mediante un omeomorfismo ad uno scorrimento di Bernoulli.
È chiaro che questa definizione è troppo restrittiva, visto che già un intreccio eteroclinico produce una dinamica simbolica più complicata di quella del teorema del punto omoclinico trasversale. Sarebbe però possibile, anche se non è il caso di farlo qui, dare una definizione più generale di dinamica simbolica con un numero finito (ma magari maggiore di due) di simboli, e di scorrimenti ristretti (non tutte le sequenze sono possibili) in modo da includere tutti i tipi di intrecci omoclinici ed eteroclinici trasversali. Definizioni di questo tipo comportano difficoltà tecniche notevoli, anche solo per essere enunciate. Tuttavia hanno il vantaggio di indicare un comportamento dinamico ben definito, di cui esiste una descrizione esplicita.
Il problema sorge quando ci si chiede ``quante sono'' le condizioni
iniziali che danno luogo al caos nel senso di questa definizione molto
restrittiva. Si noti che gli insiemi di Smale
![]() hanno misura zero. Perciò la difficoltà associata a questo tipo di
definizione è far vedere che esistono insiemi abbastanza grandi, per
esempio nel senso della loro area, di condizioni iniziali caotiche.
hanno misura zero. Perciò la difficoltà associata a questo tipo di
definizione è far vedere che esistono insiemi abbastanza grandi, per
esempio nel senso della loro area, di condizioni iniziali caotiche.
Un'alternativa che è stata discussa a lungo è una definizione di regione caotica che faccia riferimento alle sue proprietà qualitative, al fatto che le orbite vadano ``ognuna per conto suo'', in termini intuitivi il caos definito come assenza di ordine. Senza addentrarci nelle difficoltà di una definizione di natura così qualitativa, proviamo a dare una definizione semplice di questo tipo.
Definizione:
Un'orbita presenta il fenomeno del caos se essa non è né un punto fisso ellittico, né un punto periodico ellittico, né una curva invariante di Moser.
Questo tentativo di definire il caos per negazione, elencando i casi che non sono da considerare caotici, non risolve il problema di definire una regione caotica in modo operativo. Come abbiamo visto le regioni ordinate non hanno punti interni, quindi si mescolano alle regioni caotiche in ogni intorno, arbitrariamente piccolo. Inoltre una definizione negativa non permette di ottenere molti risultati: le orbite che non sono né periodiche né del tipo descritto dal teorema di Moser possono avere un comportamento del tutto diverso da quelli delle orbite caotiche note, come quelle descritte dalla dinamica simbolica.
Riassumendo i tentativi di questa Sezione per dare una definizione di caos, notiamo che le tre ipotesi fatte qua sopra sono legate tra loro come segue.
Un punto su di un insieme iperbolico ha esponenti di Lyapounov positivi e negativi. Le curve invarianti di Moser hanno esponenti di Lyapounov tutti nulli. Perciò la definizione di caos basata sugli insiemi iperbolici e la dinamica simbolica è la più restrittiva, che implica le altre. La definizione di caos basata sui soli esponenti di Lyapounov è intermedia tra le altre due, cioè implica quella basata sull'assenza di ordine ed è implicata da quella basata sugli insiemi iperbolici. La definizione di caos come ``non ordine'' è la più vaga, cioè contiene meno informazione.
In conclusione, non si conosce ancora una definizione di caos che sia pienamente soddisfacente. Questo concetto è stato indagato ormai per più di un secolo, eppure la sua complessità, e quindi la ricchezza della ricerca matematica che resta da svolgere su di esso, non finiscono di stupirci.
Gli studenti dei corsi di laurea in matematica o di altre materie, come fisica, in cui ha molto peso il rigore logico, non sono abituati a sentirsi dire che non si sa come definire in modo soddisfacente un concetto fondamentale. Ma la frontiera della ricerca matematica è piena di esempi di questo genere. Per questo mi è sembrato utile concludere questo testo in questo modo.
Andrea Milani 2009-06-01