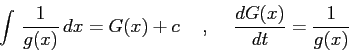Subsections
1.2 SISTEMI LINEARI, INTEGRABILITÀ
Sommario La legge che governa il moto, sia essa un campo vettoriale
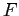 o una mappa
o una mappa 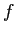 , può essere lineare o nonlineare. Nel caso
lineare è possibile esprimere tutte le orbite in modo
relativamente semplice, utilizzando funzioni trascendenti
elementari. Nel caso nonlineare questo non è in generale
possibile, e bisogna accontentarsi di una descrizione incompleta,
di tipo qualitativo.
, può essere lineare o nonlineare. Nel caso
lineare è possibile esprimere tutte le orbite in modo
relativamente semplice, utilizzando funzioni trascendenti
elementari. Nel caso nonlineare questo non è in generale
possibile, e bisogna accontentarsi di una descrizione incompleta,
di tipo qualitativo.
Esempio:
L'esempio più semplice di sistema dinamico continuo
si ottiene in dimensione  , per
, per 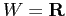 , e con per campo
vettoriale una funzione lineare omogenea:
, e con per campo
vettoriale una funzione lineare omogenea:
L'orbita 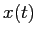 che passa per la condizione iniziale
che passa per la condizione iniziale 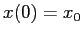 si
può esprimere mediante una funzione esponenziale:
si
può esprimere mediante una funzione esponenziale:
Questa orbita è l'unica che passa per 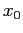 al tempo
al tempo 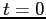 :
infatti, se
:
infatti, se 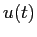 fosse un'altra soluzione con
fosse un'altra soluzione con 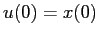 :
:
per cui
Esempio:
L'analogo sistema dinamico discreto è il sistema in
dimensione  in cui la mappa è lineare omogenea:
in cui la mappa è lineare omogenea:
L'orbita con condizione iniziale 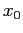 assegnata si esprime con
una funzione polinomiale:
assegnata si esprime con
una funzione polinomiale:
Anche in questo caso l'unicità dell'orbita con condizione iniziale
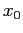 è immediata: se
è immediata: se 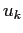 fosse un'altra orbita con
fosse un'altra orbita con 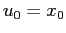 ,
allora:
,
allora:
La relazione tra i due esempi, di sistema lineare continuo e
discreto, si ottiene mediante la discretizzazione del tempo 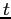 ,
cioè costruendo una successione di tempi, e di valori dello stato a
questi corrispondenti. Il caso più semplice è quello in cui la
discretizzazione ha un passo
costante
,
cioè costruendo una successione di tempi, e di valori dello stato a
questi corrispondenti. Il caso più semplice è quello in cui la
discretizzazione ha un passo
costante 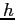 :
:
Allora il sistema discreto si costruisce a partire dal sistema
continuo:
e la mappa discreta è:
Se si conoscono le orbite di un sistema continuo, in qualche
forma esplicita, non c'è alcuna difficoltà a ricavarne un
sistema discreto, per esempio con la discretizzazione
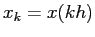 . Viceversa, il problema interessante è come scegliere
un sistema discreto che approssimi un sistema continuo, al fine di
ottenere qualche informazione sulle sue orbite: questo è
l'argomento del capitolo 4.
. Viceversa, il problema interessante è come scegliere
un sistema discreto che approssimi un sistema continuo, al fine di
ottenere qualche informazione sulle sue orbite: questo è
l'argomento del capitolo 4.
Un esempio appena meno semplice si ottiene in dimensione 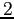 mettendo insieme (mediante un prodotto cartesiano) due equazioni
lineari in dimensione 1.
Esempio:
mettendo insieme (mediante un prodotto cartesiano) due equazioni
lineari in dimensione 1.
Esempio:
Le orbite si ottengono risolvendo separatamente le due equazioni per
le variabili 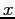 ed
ed 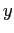 che sono disaccoppiate:
che sono disaccoppiate:
esprime tutte le orbite in
funzione della condizione iniziale
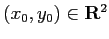 .
.
Definizione:
Il flusso integrale (detto anche soluzione generale) di
un sistema dinamico continuo è la famiglia ad un parametro di
applicazioni
che per ogni tempo
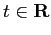 mandano la condizione iniziale
mandano la condizione iniziale 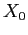 nel valore
della corrispondente soluzione al tempo
nel valore
della corrispondente soluzione al tempo 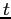 .
.
Nell'esempio qui sopra, il flusso integrale è noto esplicitamente
mediante la sua espressione analitica (a base di esponenziali); in
questo senso il sistema dinamico è integrabile.
È anche possibile ottenere dell'informazione qualitativa, per
esempio sullo stato asintotico del sistema dinamico, cioè calcolare
i limiti per
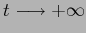 e per
e per
 . Per il sistema dinamico dell'esempio qui sopra, i limiti
dipendono solo dalla condizione iniziale e dal segno di
. Per il sistema dinamico dell'esempio qui sopra, i limiti
dipendono solo dalla condizione iniziale e dal segno di 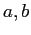 :
Esempio:
:
Esempio:
Per ogni condizione iniziale:
mentre per ogni condizione iniziale diversa da
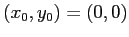 :
:
dove il simbolo 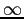 indica limite infinito in
indica limite infinito in 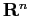 .
Il caso con
.
Il caso con 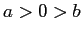 è un po' più complicato; se
è un po' più complicato; se 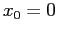 anche
anche
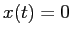 :
:
mentre per tutte le altre condizioni iniziali:
Esercizio
Trovare i limiti per
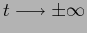 in tutti gli altri
casi.
(Soluzione)
in tutti gli altri
casi.
(Soluzione)
Benché l'esempio qui sopra sia un caso molto semplice, è possibile
ricondursi ad un caso altrettanto semplice per una classe di sistemi
dinamici:
Definizione:
Un sistema dinamico continuo si dice lineare quando il campo
vettoriale a secondo membro è lineare, cioè se è della forma:
con
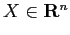 ,
, 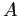 una matrice
una matrice 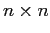 a coefficienti costanti.
a coefficienti costanti.
Come vedremo nella Sezione 2.3, tutti i sistemi
dinamici lineari si possono ricondurre all'esempio qua sopra quando
la matrice 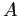 è diagonalizzabile.
è diagonalizzabile.
Un sistema dinamico continuo si dice nonlineare, se è
della forma
con 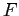 non lineare; in tal caso è in generale difficile da
risolvere (nel senso di descrivere esplicitamente il
flusso integrale).
non lineare; in tal caso è in generale difficile da
risolvere (nel senso di descrivere esplicitamente il
flusso integrale).
Esempio:
Le soluzioni ottenute nell'esempio qui sopra, malgrado si tratti
dell'esempio più semplice possibile di sistema dinamico
nonlineare, non sono esplicite nello stesso senso delle soluzioni di
un sistema dinamico lineare:
- Prima di tutto occorre eseguire una quadratura, o calcolo di
primitiva: come è noto esistono funzioni con espressioni
analitiche molto semplici, le cui primitive non hanno un'espressione
analitica finita come composizione di funzioni
elementari (esempio:
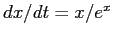 ).
).
- In secondo luogo occorre invertire la primitiva, e l'inversa di
una funzione con espressione analitica semplice non è detto che
sia esprimibile come composizione di funzioni
elementari (esempio:
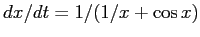 ).
).
Esercizio
Scrivere tutte le soluzioni di:
Questo sistema dinamico ha soluzioni definite per ogni 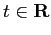 ?
(Soluzione)
?
(Soluzione)
Esercizio
Scrivere tutte le soluzioni di:
Questo sistema dinamico ha
soluzioni definite per ogni 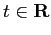 ?
(Soluzione)
?
(Soluzione)
Un sistema dinamico nonlineare può essere non integrabile in un
senso più forte, cioè la soluzione può non essere
esprimibile neppure con quadrature ed inversioni; in generale questo
si verifica anche in dimensione 2, cioè per un sistema dinamico
della forma:
dove
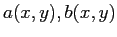 sono
funzioni nonlineari. Per questo nel caso di sistemi dinamici nonlineari
si può essere costretti a limitarsi ad uno studio qualitativo delle
soluzioni, come discusso nel capitolo 3.
sono
funzioni nonlineari. Per questo nel caso di sistemi dinamici nonlineari
si può essere costretti a limitarsi ad uno studio qualitativo delle
soluzioni, come discusso nel capitolo 3.
Andrea Milani
2009-06-01
![]() o una mappa
o una mappa ![]() , può essere lineare o nonlineare. Nel caso
lineare è possibile esprimere tutte le orbite in modo
relativamente semplice, utilizzando funzioni trascendenti
elementari. Nel caso nonlineare questo non è in generale
possibile, e bisogna accontentarsi di una descrizione incompleta,
di tipo qualitativo.
, può essere lineare o nonlineare. Nel caso
lineare è possibile esprimere tutte le orbite in modo
relativamente semplice, utilizzando funzioni trascendenti
elementari. Nel caso nonlineare questo non è in generale
possibile, e bisogna accontentarsi di una descrizione incompleta,
di tipo qualitativo. 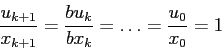
![]() . Viceversa, il problema interessante è come scegliere
un sistema discreto che approssimi un sistema continuo, al fine di
ottenere qualche informazione sulle sue orbite: questo è
l'argomento del capitolo 4.
. Viceversa, il problema interessante è come scegliere
un sistema discreto che approssimi un sistema continuo, al fine di
ottenere qualche informazione sulle sue orbite: questo è
l'argomento del capitolo 4.
![]() mettendo insieme (mediante un prodotto cartesiano) due equazioni
lineari in dimensione 1.
Esempio:
mettendo insieme (mediante un prodotto cartesiano) due equazioni
lineari in dimensione 1.
Esempio:
![]() ed
ed ![]() che sono disaccoppiate:
che sono disaccoppiate:
![]() e per
e per
![]() . Per il sistema dinamico dell'esempio qui sopra, i limiti
dipendono solo dalla condizione iniziale e dal segno di
. Per il sistema dinamico dell'esempio qui sopra, i limiti
dipendono solo dalla condizione iniziale e dal segno di ![]() :
Esempio:
:
Esempio:
![]() in tutti gli altri
casi.
(Soluzione)
in tutti gli altri
casi.
(Soluzione)
![]() è diagonalizzabile.
è diagonalizzabile.