PROBLEMA 3.1 Usiamo la foma canonica di Jordan
dove
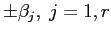 e
e 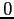 con molteplicità
con molteplicità 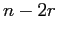 sono gli autovalori di
sono gli autovalori di 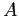 , tutti con parte reale nulla, ed
, tutti con parte reale nulla, ed 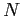 è una matrice nilpotente di un certo ordine
è una matrice nilpotente di un certo ordine 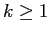 . Poiché
. Poiché 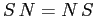
dove 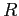 è una matrice di rotazione, che conserva la norma euclidea dei vettori, ed
è una matrice di rotazione, che conserva la norma euclidea dei vettori, ed 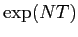 ha coefficienti che sono monomi in
ha coefficienti che sono monomi in 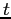 di grado fino a
di grado fino a 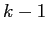 . Allora data la condizione iniziale nelle coordinate della forma canonica
. Allora data la condizione iniziale nelle coordinate della forma canonica 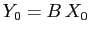 la norma
la norma
tende all'infinito per
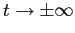 perché alcune componenti devono contenere il monomio
perché alcune componenti devono contenere il monomio 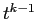 , e quindi esistono condizioni iniziali in ogni intorno dell'origine per le quali
, e quindi esistono condizioni iniziali in ogni intorno dell'origine per le quali 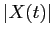 tende all'infinito.
tende all'infinito.
ESERCIZIO 3.2 Il linearizzato in 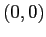 ha matrice
ha matrice
con equazione caratteristica
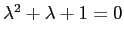 ed autovalori
ed autovalori
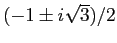 , quindi l'unico esponente di Lyapounov è
, quindi l'unico esponente di Lyapounov è 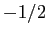 e l'origine è un pozzo nonlineare.
e l'origine è un pozzo nonlineare.
ESERCIZIO 3.3 I punti di equilibrio si individuano risolvendo
da cui i punti di equilibrio sono
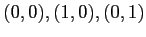 . La stabilità si studia linearizzando
. La stabilità si studia linearizzando 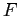 in questi tre punti, cioè usando la matrice jacobiana
in questi tre punti, cioè usando la matrice jacobiana
Si ottiene che 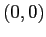 è un pozzo,
è un pozzo, 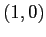 ha autovalori di segno opposto, cioè è una sella.
ha autovalori di segno opposto, cioè è una sella. 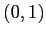 ha un autovalore nullo e uno positivo quindi la sua stabilità non può essere determinata sulla base del solo calcolo degli esponenti di Lyapounov (ma è instabile per ragioni che saranno chiare dopo la Sezione 3.6.)
ha un autovalore nullo e uno positivo quindi la sua stabilità non può essere determinata sulla base del solo calcolo degli esponenti di Lyapounov (ma è instabile per ragioni che saranno chiare dopo la Sezione 3.6.)
ESERCIZIO 3.4 Il sistema linearizzato nell'origine è
gli autovalori sono immaginari puri, ed è necessario cercare una funzione di Lyapounov 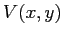 per l'origine. Ha successo il tentativo
per l'origine. Ha successo il tentativo
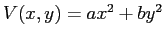 , con
, con 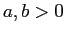 : affinché
: affinché
 basta che
basta che  .
.
ESERCIZIO 3.5 La funzione
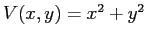 è una funzione di Lyapounov decrescente su tutto
è una funzione di Lyapounov decrescente su tutto 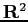 . Infatti
. Infatti
è  ovunque, e
ovunque, e 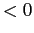 per
per 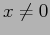 . Ma dove
. Ma dove 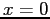 , escludendo l'origine, si ha
, escludendo l'origine, si ha 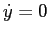 e
e 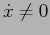 , quindi le orbite attraversano la retta
, quindi le orbite attraversano la retta 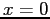 con velocità non nulla, e
con velocità non nulla, e 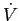 è nullo per un singolo valore di
è nullo per un singolo valore di 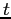 , quindi
, quindi 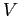 è decrescente su ogni orbita diversa dal punto di equilibrio. Il teorema della funzione di Lyapounov decrescente si applica con
è decrescente su ogni orbita diversa dal punto di equilibrio. Il teorema della funzione di Lyapounov decrescente si applica con 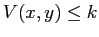 come insieme positivamente invariante, per ogni
come insieme positivamente invariante, per ogni 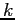 .
.
ESERCIZIO 3.6 L'energia potenziale si ottiene per quadratura:
ha un massimo in 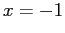 e un minimo in
e un minimo in 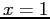 ; inoltre
; inoltre
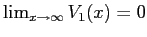 . Quindi
. Quindi 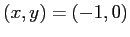 è una sella,
è una sella, 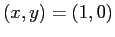 è stabile.
è stabile.
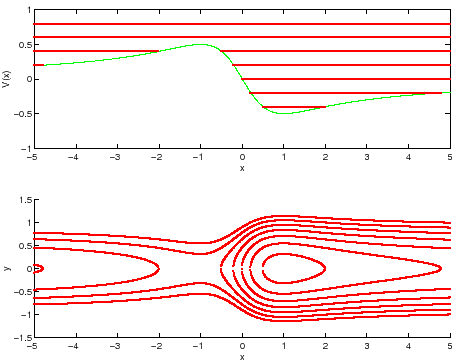
Figura C.1:
curve di livello per l'energia potenziale 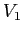 .
.
 |
ha un minimo per 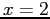 ,
,
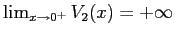 e
e
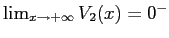 . Quindi
. Quindi 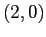 è stabile.
è stabile.
Figura C.2:
curve di livello per l'energia potenziale 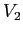 .
.
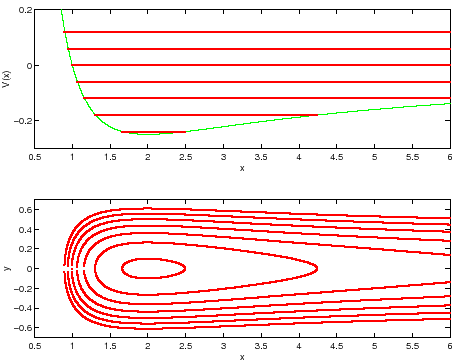 |
PROBLEMA 3.7 Le radici reali dell'equazione di terzo grado sono 1,2 o 3. Se c'è una sola radice, corrisponde ad un massimo di 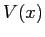 per
per 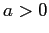 , quindi c'è un solo punto di equilibrio che è una sella; se
, quindi c'è un solo punto di equilibrio che è una sella; se 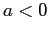 c'è solo un minimo di
c'è solo un minimo di 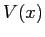 , corrispondente ad un equilibrio stabile. Se ci sono 3 radici reali, con
, corrispondente ad un equilibrio stabile. Se ci sono 3 radici reali, con 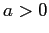 ,
, 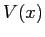 ha due massimi ed un minimo, e il comportamento qualitativo dipende anche da quale dei due massimi ha un valore più alto, perchè le separatrici della sella corrispondente al massimo assoluto stanno ``al di fuori'' di quelle dell'altro massimo. Con
ha due massimi ed un minimo, e il comportamento qualitativo dipende anche da quale dei due massimi ha un valore più alto, perchè le separatrici della sella corrispondente al massimo assoluto stanno ``al di fuori'' di quelle dell'altro massimo. Con 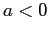 e tre radici, ci sono due minimi (corrispondenti a due equilibri stabili) e un massimo; la corrispondente sella ha separatrici che si richiudono attorno ai due equilibri stabili. Se ci sono due radici, una deve essere doppia e
e tre radici, ci sono due minimi (corrispondenti a due equilibri stabili) e un massimo; la corrispondente sella ha separatrici che si richiudono attorno ai due equilibri stabili. Se ci sono due radici, una deve essere doppia e 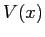 ha un flesso a tangente orizzontale, quindi la figura è localmente come quella a destra in Figura 3.2.
ha un flesso a tangente orizzontale, quindi la figura è localmente come quella a destra in Figura 3.2.
ESERCIZIO 3.8 a) I punti di equilibrio sono
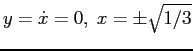 ; la matrice jacobiana è
; la matrice jacobiana è
e quindi
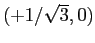 ha un linearizzato di tipo sella, mentre
ha un linearizzato di tipo sella, mentre
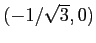 è un pozzo. L'energia totale del problema con
è un pozzo. L'energia totale del problema con 
(dove la costante è stata aggiustata per avere
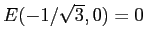 ) è una funzione di Lyapounov per il pozzo
) è una funzione di Lyapounov per il pozzo
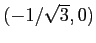 , decrescente su qualunque insieme che escluda la sella
, decrescente su qualunque insieme che escluda la sella
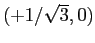 . La componente connessa contenente il pozzo di un insieme
. La componente connessa contenente il pozzo di un insieme 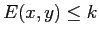 per una qualsiasi costante
per una qualsiasi costante 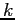 tale che
tale che
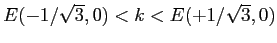 è un compatto positivamente invariante su cui
è un compatto positivamente invariante su cui 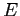 è una funzione di Lyapounov decrescente, per cui appartiene al bacino.
è una funzione di Lyapounov decrescente, per cui appartiene al bacino.
b) I punti di equlibrio sono
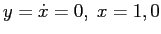 ; la matrice jacobiana è
; la matrice jacobiana è
e quindi 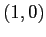 ha un linearizzato di tipo sella, mentre
ha un linearizzato di tipo sella, mentre 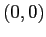 ha un linearizzato degenere, con determinante nullo e autovalori
ha un linearizzato degenere, con determinante nullo e autovalori 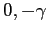 . Perciò non ci sono pozzi.
. Perciò non ci sono pozzi.
PROBLEMA 3.9 Nei punti in cui 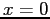 si ha pure
si ha pure 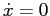 , per cui la retta
, per cui la retta 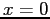 è un insieme invariante, e su questa retta il sistema dinamico è
è un insieme invariante, e su questa retta il sistema dinamico è
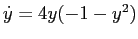 che ha un pozzo in
che ha un pozzo in 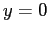 . L'insieme
. L'insieme 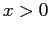 è invariante e contiene un solo punto di equilibrio
è invariante e contiene un solo punto di equilibrio 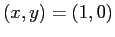 che ha la funzone di Lyapounov stretta
che ha la funzone di Lyapounov stretta 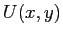 , ed insiemi positivamente invarianti compatti definit da
, ed insiemi positivamente invarianti compatti definit da 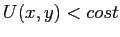 . Quindi per il teorema della funzione di Lyapounov decrescente
. Quindi per il teorema della funzione di Lyapounov decrescente 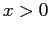 è il bacino di
è il bacino di 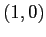 . Lo stesso ragionamento per
. Lo stesso ragionamento per 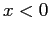 che è il bacino di
che è il bacino di 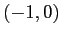 .
.
ESERCIZIO 3.10 Con un cambiamento di coordinate lineare (una rotazione) si può diagonalizzare la matrice simmetrica che definisce la forma quadratica; nelle nuove coordinate la forma quadratica diventa
con
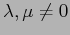 perché la forma quadratica è non degenere. Quindi nelle nuove coordinate il sistema dinamico è
perché la forma quadratica è non degenere. Quindi nelle nuove coordinate il sistema dinamico è
che è una sorgente, sella o pozzo a seconda dei segni di  e
e 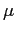 .
.
ESERCIZIO 3.11 Poiché
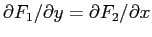 su tutto
su tutto 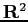 che è semplicemente connesso, si tratta di un sistema gradiente. Per determinare
che è semplicemente connesso, si tratta di un sistema gradiente. Per determinare 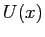 in modo che
in modo che 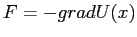 : integrando su una curva
: integrando su una curva 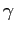 che congiunge
che congiunge 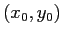 e
e 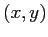 in
in 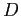 , (per esempio
, (per esempio
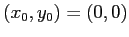 e
e
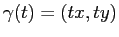 ) si ottiene
) si ottiene
e per  ,
,
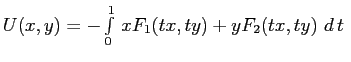 . Perciò
. Perciò
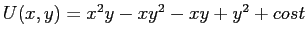 ; i punti critici del potenziale sono
; i punti critici del potenziale sono
Calcolando le matrici hessiane, si trova che ci sono tre selle ed un minimo; per cui i punti di equilibrio sono tre selle ed un pozzo.
ESERCIZIO 3.12 I punti di equilibrio sono due:
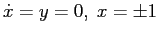 con linearizzato rispettivamente
con linearizzato rispettivamente
quindi  è un pozzo nonlineare per ogni
è un pozzo nonlineare per ogni 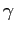 , mentre
, mentre 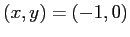 è una sella nonlineare con separatrice stabile e instabile tangenti rispettivamente a
è una sella nonlineare con separatrice stabile e instabile tangenti rispettivamente a
L'andamento delle separatrici è descritto nella Figura C.3, il bacino di attrazione del pozzo è indicato con la lettera 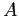 .
.
Un programma di calcolo per calcolare con buona approssimazione le separatrici del punto di sella è esesepar.m ; sono però necessarie anche le due subroutines esesep.m e esesepm.m per calcolare il secondo membro delle equazioni differenziali sia in avanti che indietro. In sostanza il principio applicato per tracciare le separatrici è lo stesso usato per il caso discreto nella Sezione 6.1.
Figura C.3:
Separatrice stabile (verde) e instabile (rosso).
 |
PROBLEMA 3.13 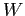 è positivamente invariante, ed essendo compatto le condizioni iniziali in
è positivamente invariante, ed essendo compatto le condizioni iniziali in 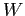 corrispondono a soluzioni definite per ogni
corrispondono a soluzioni definite per ogni 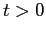 . Quindi esistono gli insiemi
. Quindi esistono gli insiemi 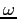 -limite e, non essendoci equilibri in
-limite e, non essendoci equilibri in 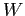 , per il teorema di Poincaré-Bendixon questi insiemi limite sono orbite periodiche.
, per il teorema di Poincaré-Bendixon questi insiemi limite sono orbite periodiche.
ESERCIZIO 3.14 La curva 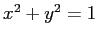 divide il piano nell'interno
divide il piano nell'interno
 e l'esterno
e l'esterno
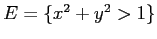 . Se
. Se 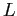 fosse un insieme limite sarebbe anche invariante, e quindi sarebbe invariante l'esterno
fosse un insieme limite sarebbe anche invariante, e quindi sarebbe invariante l'esterno 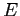 . Ogni soluzione contenuta nell'esterno
. Ogni soluzione contenuta nell'esterno 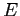 non potrebbe avere valori limite contenuti in
non potrebbe avere valori limite contenuti in 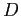 , quindi i punti
, quindi i punti 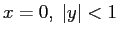 non possono appartenere all'
non possono appartenere all'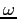 -limite. Analogamente, la curva chiusa formata da una delle due semicirconferenze e dal diametro divide il piano in un interno ed un esterno, con interno invariante se
-limite. Analogamente, la curva chiusa formata da una delle due semicirconferenze e dal diametro divide il piano in un interno ed un esterno, con interno invariante se 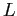 è invariante. Una soluzione contenuta nell'interno non potrebbe avere punti limite appartenenti all'altra metà della circonferenza.
è invariante. Una soluzione contenuta nell'interno non potrebbe avere punti limite appartenenti all'altra metà della circonferenza.
Andrea Milani
2009-06-01
![]() ha matrice
ha matrice
![\begin{displaymath}A=\left[\begin{array}{cc}{-1}&{1}\\
{-1}&{0}\end{array}\right] \end{displaymath}](img2731.png)
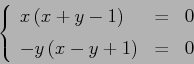
![\begin{displaymath}\frac{\partial {(\dot x, \dot y)}}{\partial {(x,y)}}= \left[\...
...cc}{2x+y-1}&{x}\\
{-y}&{2y-x-1}\end{array}\right] =A(x,y)\ . \end{displaymath}](img2737.png)
![\begin{displaymath}\left[\begin{array}{c}{\dot x}\\
{\dot y}\end{array}\right]...
...y}\right]\left[\begin{array}{c}{x}\\
{y}\end{array}\right]\; \end{displaymath}](img2739.png)
![]() è una funzione di Lyapounov decrescente su tutto
è una funzione di Lyapounov decrescente su tutto ![]() . Infatti
. Infatti
![]() per
per ![]() , quindi c'è un solo punto di equilibrio che è una sella; se
, quindi c'è un solo punto di equilibrio che è una sella; se ![]() c'è solo un minimo di
c'è solo un minimo di ![]() , corrispondente ad un equilibrio stabile. Se ci sono 3 radici reali, con
, corrispondente ad un equilibrio stabile. Se ci sono 3 radici reali, con ![]() ,
, ![]() ha due massimi ed un minimo, e il comportamento qualitativo dipende anche da quale dei due massimi ha un valore più alto, perchè le separatrici della sella corrispondente al massimo assoluto stanno ``al di fuori'' di quelle dell'altro massimo. Con
ha due massimi ed un minimo, e il comportamento qualitativo dipende anche da quale dei due massimi ha un valore più alto, perchè le separatrici della sella corrispondente al massimo assoluto stanno ``al di fuori'' di quelle dell'altro massimo. Con ![]() e tre radici, ci sono due minimi (corrispondenti a due equilibri stabili) e un massimo; la corrispondente sella ha separatrici che si richiudono attorno ai due equilibri stabili. Se ci sono due radici, una deve essere doppia e
e tre radici, ci sono due minimi (corrispondenti a due equilibri stabili) e un massimo; la corrispondente sella ha separatrici che si richiudono attorno ai due equilibri stabili. Se ci sono due radici, una deve essere doppia e ![]() ha un flesso a tangente orizzontale, quindi la figura è localmente come quella a destra in Figura 3.2.
ha un flesso a tangente orizzontale, quindi la figura è localmente come quella a destra in Figura 3.2.
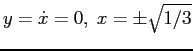 ; la matrice jacobiana è
; la matrice jacobiana è
![\begin{displaymath}\frac{\partial {(\dot x, \dot y)}}{\partial {(x,y)}}=\left[\begin{array}{cc}{0}&{1}\\
{6x}&{-\gamma}\end{array}\right] \end{displaymath}](img2764.png)
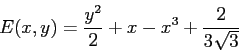
![\begin{displaymath}\frac{\partial {(\dot x, \dot y)}}{\partial {(x,y)}}=\left[\begin{array}{cc}{0}&{1}\\
{3x^2-2x}&{-\gamma}\end{array}\right] \end{displaymath}](img2771.png)
![]() si ha pure
si ha pure ![]() , per cui la retta
, per cui la retta ![]() è un insieme invariante, e su questa retta il sistema dinamico è
è un insieme invariante, e su questa retta il sistema dinamico è
![]() che ha un pozzo in
che ha un pozzo in ![]() . L'insieme
. L'insieme ![]() è invariante e contiene un solo punto di equilibrio
è invariante e contiene un solo punto di equilibrio ![]() che ha la funzone di Lyapounov stretta
che ha la funzone di Lyapounov stretta ![]() , ed insiemi positivamente invarianti compatti definit da
, ed insiemi positivamente invarianti compatti definit da ![]() . Quindi per il teorema della funzione di Lyapounov decrescente
. Quindi per il teorema della funzione di Lyapounov decrescente ![]() è il bacino di
è il bacino di ![]() . Lo stesso ragionamento per
. Lo stesso ragionamento per ![]() che è il bacino di
che è il bacino di ![]() .
.
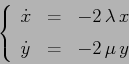
![]() su tutto
su tutto ![]() che è semplicemente connesso, si tratta di un sistema gradiente. Per determinare
che è semplicemente connesso, si tratta di un sistema gradiente. Per determinare ![]() in modo che
in modo che ![]() : integrando su una curva
: integrando su una curva ![]() che congiunge
che congiunge ![]() e
e ![]() in
in ![]() , (per esempio
, (per esempio
![]() e
e
![]() ) si ottiene
) si ottiene
![\begin{displaymath}-U\left (s\left[\begin{array}{c}{x}\\
{y}\end{array}\right]...
...y}{c}{x}\\
{y}\end{array}\right]\right )\right\}\,\,d\,{t}\; \end{displaymath}](img2785.png)
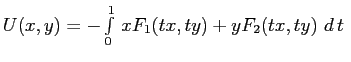 . Perciò
. Perciò
![\begin{displaymath}\left[\begin{array}{c}{1}\\
{1}\end{array}\right]\;,\; \lef...
...\; \left[\begin{array}{c}{2/3}\\
{1/3}\end{array}\right] \ . \end{displaymath}](img2789.png)
![]() con linearizzato rispettivamente
con linearizzato rispettivamente
![\begin{displaymath}\left.\frac{\partial {(\dot x, \dot y)}}{\partial {(x,y)}}\ri...
...t[\begin{array}{cc}{0}&{1}\\
{2}&{-\gamma}\end{array}\right] \end{displaymath}](img2791.png)

![]() è positivamente invariante, ed essendo compatto le condizioni iniziali in
è positivamente invariante, ed essendo compatto le condizioni iniziali in ![]() corrispondono a soluzioni definite per ogni
corrispondono a soluzioni definite per ogni ![]() . Quindi esistono gli insiemi
. Quindi esistono gli insiemi ![]() -limite e, non essendoci equilibri in
-limite e, non essendoci equilibri in ![]() , per il teorema di Poincaré-Bendixon questi insiemi limite sono orbite periodiche.
, per il teorema di Poincaré-Bendixon questi insiemi limite sono orbite periodiche.
![]() divide il piano nell'interno
divide il piano nell'interno
![]() e l'esterno
e l'esterno
![]() . Se
. Se ![]() fosse un insieme limite sarebbe anche invariante, e quindi sarebbe invariante l'esterno
fosse un insieme limite sarebbe anche invariante, e quindi sarebbe invariante l'esterno ![]() . Ogni soluzione contenuta nell'esterno
. Ogni soluzione contenuta nell'esterno ![]() non potrebbe avere valori limite contenuti in
non potrebbe avere valori limite contenuti in ![]() , quindi i punti
, quindi i punti ![]() non possono appartenere all'
non possono appartenere all'![]() -limite. Analogamente, la curva chiusa formata da una delle due semicirconferenze e dal diametro divide il piano in un interno ed un esterno, con interno invariante se
-limite. Analogamente, la curva chiusa formata da una delle due semicirconferenze e dal diametro divide il piano in un interno ed un esterno, con interno invariante se ![]() è invariante. Una soluzione contenuta nell'interno non potrebbe avere punti limite appartenenti all'altra metà della circonferenza.
è invariante. Una soluzione contenuta nell'interno non potrebbe avere punti limite appartenenti all'altra metà della circonferenza.