A large fraction of the asteroids have been lost shortly
after discovery, thus the asteroid catalogs contain a large number of
low accuracy orbits. Two of these inaccurate orbits can belong to the
same physical object; the challenge is to find effective algorithms
for identification. We give a new method to propose identifications of
orbits, applicable in the case where each of the two observed arcs
provides enough information to solve for all the orbital elements by a
least squares fit to the observations.
Even if the optimum fit solution is unique, there is a confidence
region in the space of orbital elements containing orbital solutions
compatible with the observations: the identification of orbits is the
search for an orbital solution in the intersection of the two
confidence regions. In the linear approximation there is a rigorous
and simple algorithm to find the optimum joint solution and the
increase in the RMS of the residuals relative to the two separate
solutions. The linear approximation may fail if two poorly determined
orbits are too far apart in the orbital elements space. In this case,
the linear algorithm becomes more stable when restricted to only some
of the orbital elements.
Our procedure proposes orbit identification using a cascade of tests,
all based upon identification metrics taking into account the
difference in the orbits weighted with the uncertainty. The first test
is based only upon the orbital plane; the couples of orbits compatible
according to the first test are submitted to further tests using
identification metrics based upon 5 and 6 orbital elements. Finally,
the couples passing all tests are submitted to an accurate
computation, by differential correction, of the orbit fitting both
sets of observations. This procedure has been tested on a set of 100
already known identifications, and was found to be effective in 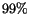 of the cases. Finally we show that these methods have been used to
obtain 150 previously unknown orbit identifications.
of the cases. Finally we show that these methods have been used to
obtain 150 previously unknown orbit identifications.
Keywords: asteroids, orbits, celestial mechanics.
Running title: Proposing Asteroid Identifications