


Next: 3. Results
Up: 2. Synthetic theory
Previous: 2.3 Fourier analysis
2.4 Semimajor axis and Lyapunov exponents
The other proper element is proper semimajor axis ap, which in
principle is obtained by removing the short periodic perturbations
from the time series of the osculating a. A rigorous definition
would be somewhat more complicated than just the average of a(t),
because of second order perturbations which contain both constant and
long periodic terms (Milani et al. [1987]). However, the
second order perturbations are very small and in practice they are
seldom the main source of time variation of the proper semimajor axis:
chaotic effects are dominant in most cases. For this reason we have
not attempted to perform second order corrections, and we have
computed ap as the mean of the values of a(t) as it came out of
the digital filter; that is, we are taking a mean of the already
smoothed data. Stability tests are done again by the running box
method.
There is a third proper frequency, fp, which is the slope of the
angle
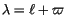 .
Note that in our numerical integration
code the output for
.
Note that in our numerical integration
code the output for 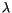 includes the principal value in
includes the principal value in ![$[0,
2\pi]$](img48.gif) and the number of revolutions completed since the initial
conditions, thus the value of fp can be obtained by a simple linear
fit to the filtered
and the number of revolutions completed since the initial
conditions, thus the value of fp can be obtained by a simple linear
fit to the filtered 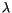 ;
the filter also preserves the number of
revolutions. Stability of fp is tested by the running box
method. In principle we can define a ``mean mean motion'' np=fp-g
as the proper frequency of the mean anomaly
;
the filter also preserves the number of
revolutions. Stability of fp is tested by the running box
method. In principle we can define a ``mean mean motion'' np=fp-g
as the proper frequency of the mean anomaly  ;
however, the
frequency np is not related to ap by Kepler's third law. The
mean anomaly contains not only perturbations acting
through changes in a, but also because of the accumulated effect of
the perturbations in a (this is the classical double integration
argument). In practice large deviations of
;
however, the
frequency np is not related to ap by Kepler's third law. The
mean anomaly contains not only perturbations acting
through changes in a, but also because of the accumulated effect of
the perturbations in a (this is the classical double integration
argument). In practice large deviations of 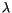 from
from
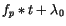 ,
let us say several revolutions, are a strong indication of
chaotic motion (Milani et al. [1997]), in particular of jumps
between different chaotic states corresponding to different values of
ap. For this reason we also use, as indicator of irregular motion,
the root mean square and the maximum difference of the residuals of
filtered
,
let us say several revolutions, are a strong indication of
chaotic motion (Milani et al. [1997]), in particular of jumps
between different chaotic states corresponding to different values of
ap. For this reason we also use, as indicator of irregular motion,
the root mean square and the maximum difference of the residuals of
filtered 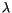 with respect to the linear fit.
A well known indicator of chaotic motion is the maximum Lyapunov
Characteristic Exponent (LCE). Although the LCE is rigorously defined
as a limit for
with respect to the linear fit.
A well known indicator of chaotic motion is the maximum Lyapunov
Characteristic Exponent (LCE). Although the LCE is rigorously defined
as a limit for
 ,
an indicator can be obtained by a finite
integration of both the equation of motion and the corresponding
variational equation. Following Milani and Nobili ([1992], we
compute an approximation of the LCE as the best fit slope of the
function of time
,
an indicator can be obtained by a finite
integration of both the equation of motion and the corresponding
variational equation. Following Milani and Nobili ([1992], we
compute an approximation of the LCE as the best fit slope of the
function of time
![$\gamma(t)= \log [D(t)/D(0)]$](img52.gif) ,
where D(t) is the
length of a variation vector (with initial conditions selected at
random). Renormalisation of the variations vector needs to be applied
when it becomes too large, to avoid numerical instability and
overflow. This method typically allows to detect a positive LCE after
7-8 Lyapunov times TL (TL is the inverse of the LCE). The
approximate values of the LCE computed in this way are reliable as
order of magnitude, unless a real state transition between two chaotic
regions takes place; the exact values are not very significant,
changes by
,
where D(t) is the
length of a variation vector (with initial conditions selected at
random). Renormalisation of the variations vector needs to be applied
when it becomes too large, to avoid numerical instability and
overflow. This method typically allows to detect a positive LCE after
7-8 Lyapunov times TL (TL is the inverse of the LCE). The
approximate values of the LCE computed in this way are reliable as
order of magnitude, unless a real state transition between two chaotic
regions takes place; the exact values are not very significant,
changes by 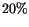 when the integration time span is extended are
typical.
when the integration time span is extended are
typical.



Next: 3. Results
Up: 2. Synthetic theory
Previous: 2.3 Fourier analysis
Andrea Milani
2000-10-03