Let us assume that the orbit with initial conditions Xi undergoes a
close approach to the Earth at a time
![]() ;
the Modified
Target Plane (MTP) for that encounter is the plane perpendicular to
the geocentric velocity at closest approach. Let this plane be
;
the Modified
Target Plane (MTP) for that encounter is the plane perpendicular to
the geocentric velocity at closest approach. Let this plane be ![]() and the points on it be
and the points on it be
![]() ;
then there is a
differentiable map
;
then there is a
differentiable map
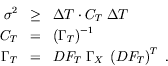
By computing the eigenvalues
![]() of
of ![]() ,
we
find that there is again a weak direction corresponding to the
long axis of the MTP ellipse. As the time elapsed from t0increases, the confidence region becomes longer and longer in the
phase space, and simultaneously thinner and thinner (this follows from
Liouville's theorem, by which the phase space 6-dimensional volume is
invariant). Thus, when a close approach takes place decades after the
initial epoch t0, the two eigenvalues of
,
we
find that there is again a weak direction corresponding to the
long axis of the MTP ellipse. As the time elapsed from t0increases, the confidence region becomes longer and longer in the
phase space, and simultaneously thinner and thinner (this follows from
Liouville's theorem, by which the phase space 6-dimensional volume is
invariant). Thus, when a close approach takes place decades after the
initial epoch t0, the two eigenvalues of ![]() have a very
large ratio. An orbital solution that moves the MTP intersection along
the weak direction results in a negligible change in the value of the
target function, that is a negligible increase in the RMS of the
observation residuals. On the contrary, a comparatively small change
in the orthogonal direction, along the minor axis of the ellipse,
would result in a significant increase of the residual RMS.
have a very
large ratio. An orbital solution that moves the MTP intersection along
the weak direction results in a negligible change in the value of the
target function, that is a negligible increase in the RMS of the
observation residuals. On the contrary, a comparatively small change
in the orthogonal direction, along the minor axis of the ellipse,
would result in a significant increase of the residual RMS.
Thus the points on the MTP which can be reached with a negligible
increase in the RMS are the points of the straight line which is the
eigenspace of the larger eigenvalue ![]() ;
let Tmin be the
point along that line that is closest to the center of the Earth,
provided it is not too far along the line (with respect to
;
let Tmin be the
point along that line that is closest to the center of the Earth,
provided it is not too far along the line (with respect to
![]() ). The distance dmin of Tmin provides an
estimate of the closest approach distance possible within the
confidence ellipsoid; this estimate involves two
approximations. First, the width
). The distance dmin of Tmin provides an
estimate of the closest approach distance possible within the
confidence ellipsoid; this estimate involves two
approximations. First, the width
![]() of the ellipse is
neglected; second, the nonlinear map FT is replaced by its
linearization DFT. Both approximations can be removed, e.g., by the
method of semilinear confidence boundaries described in
[Milani and Valsecchi 1999]. However, for the purpose of finding VIs another
approach is more efficient.
of the ellipse is
neglected; second, the nonlinear map FT is replaced by its
linearization DFT. Both approximations can be removed, e.g., by the
method of semilinear confidence boundaries described in
[Milani and Valsecchi 1999]. However, for the purpose of finding VIs another
approach is more efficient.