Resonant returns after a close approach have been discussed in different contexts, e.g., the close approaches of comet Lexell to Jupiter [Leverrier 1844] and the repeated visits to Mercury of the Mariner 10 spacecraft. B. G. Marsden recently applied this idea to the asteroid 1997 XF11 in the assumption that the 1990 precovery observations had not been discovered [Marsden 1999].
We can formulate the basic theory of resonant returns as follows. When
an asteroid undergoes a close approach in the future, decades after
the last available observation, the confidence region on the MTP is
thin, with a width much less than the diameter of the Earth and very
long; thus it is enough to perform the analysis on the long axis of
the confidence region, which we call the Line Of Variation (LOV)
[Milani 1999]. The alternate solutions along this line undergo
different degrees of perturbations, as a result of the close
approach. The elements after the encounter describe a curve in the
orbital elements space, e.g., in the (a,e) plane; the shape of such
curves can be understood by using Öpik's piecewise two body
approximation [Greenberg et al. 1988]. These curves are almost closed, they
go back to nearly the unperturbed values when the encounter is
shallow, on both extremes of the LOV [Valsecchi & Manara 1997].
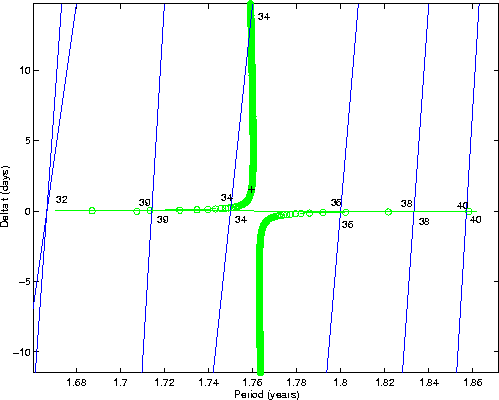
Let Pmin and Pmax be the corresponding minimum and maximum
orbital periods; every rational number in the interval between them
corresponds to at least two resonant returns. If the period P=h/kyears with h,k integers, then after h years the asteroid has
completed k orbits, the Earth has completed h orbits, and both
return to nearly the same position. As an example, 1999 AN10 can
have several different 7/4 resonant returns in 2034, resulting in an
approach potentially closer than the one in 2027, down to ![]() AU.
AU.
 |
However, two refinements must be taken into account. First, the amount
of time by which the first encounter has been missed needs to be
recovered to make the second encounter a close approach. If ![]() is the amount of time by which the asteroid is early for an encounter,
the condition to be satisfied for a resonant return at the minimum
distance is
is the amount of time by which the asteroid is early for an encounter,
the condition to be satisfied for a resonant return at the minimum
distance is
![]() ,
where
,
where ![]() and P are in
years. Thus the resonant returns are described, in the
and P are in
years. Thus the resonant returns are described, in the
![]() plane, by lines which are somewhat slanted with respect the P=h/klines. Figure 1 depicts these resonant lines for the
returns of 1999 AN10 after 2027 and for
plane, by lines which are somewhat slanted with respect the P=h/klines. Figure 1 depicts these resonant lines for the
returns of 1999 AN10 after 2027 and for ![]() .
Where these
resonance lines intersect the LOV, one finds a resonant return leading
to a close approach. In the figure the LOV has been traced by using
the multiple solutions algorithm of [Milani 1999, Sec. 5]. We have
used
.
Where these
resonance lines intersect the LOV, one finds a resonant return leading
to a close approach. In the figure the LOV has been traced by using
the multiple solutions algorithm of [Milani 1999, Sec. 5]. We have
used ![]() solutions equally spaced along the
solutions equally spaced along the ![]() axis between
-3 and +3; we have added a denser sampling of solutions along the
axis between
-3 and +3; we have added a denser sampling of solutions along the
![]() axis in the region near the 2027 closest approach. The
intersections with the resonant lines can be counted from the figure;
the resonances not touching the LOV, e.g., the P=5/3 resonance,
cannot result in deep encounters.
axis in the region near the 2027 closest approach. The
intersections with the resonant lines can be counted from the figure;
the resonances not touching the LOV, e.g., the P=5/3 resonance,
cannot result in deep encounters.
The other refinement is to consider the Minimum Orbital Intersection
Distance (MOID), the minimum distance between the two osculating
ellipses representing the orbit of the Earth and of the asteroid. Even
if the asteroid were exactly on time at the rendezvous with the Earth,
the unperturbed close approach distance cannot be less than the MOID.
For 1999 AN10, there are in fact two local MOIDs, one per node;
each is
![]() times the minimum of distance at the respective
node. If the MOID were to remain small forever, since every real
number P is approximated arbitrarily well by a rational number h/ka resonant return after h years would be always possible.
times the minimum of distance at the respective
node. If the MOID were to remain small forever, since every real
number P is approximated arbitrarily well by a rational number h/ka resonant return after h years would be always possible.
What is the evolution in time of the local MOIDs of 1999 AN10? It is not enough to compute the evolution of the MOIDs along the nominal solution, because the close approaches can change them: in particular, an encounter near the ascending node (in August) can reduce the distance at the descending node, and make possible a closer approach at the descending node (in February). We have asked G.F. Gronchi to compute the evolution of the mean orbital elements, `averaged' in the sense of [Gronchi & Milani 1998], [Gronchi & Milani 1999], in a way accounting also for the secular effects of the close approaches. The answer is that 1999 AN10 will continue to have a very low distance at both nodes for about 600 years. Thus it is simply not possible to perform close approach analyses in the sense of [Milani & Valsecchi 1999] for all possible resonant returns: there are hundreds of them.
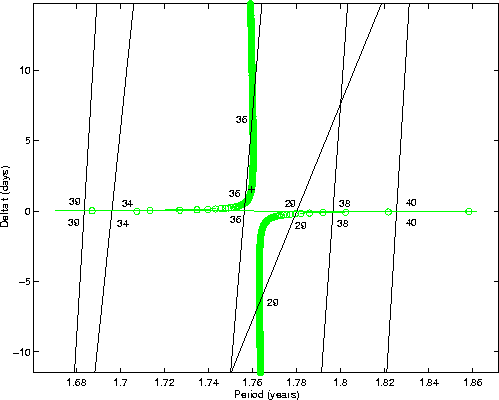 |
Because of the low nodal distance also at the descending node, there
is the possibility of a non-resonant return. This can occur if
the Earth completes h+1/2 revolutions while the asteroid completes
k+1/2 revolutions, so that they are both at the descending node at
the same time. Taking into account the eccentricities of both orbits,
the time required to go from the ascending node to the descending node
is tE for the Earth (not exactly half a year), and tA for
the asteroid (much more than half a period). Again allowing for the
timing of the 2027 encounter, the condition to be satisfied for an
encounter at the descending node is
![]() .
If we add the condition that the distance is zero at both
nodes, we have 4 conditions on the 5 variables
.
If we add the condition that the distance is zero at both
nodes, we have 4 conditions on the 5 variables
![]() ,
where u1, u2 are the eccentric anomalies at the nodes, and
we can explicitly compute tA as a function of a. Thus the above
condition defines a curve in the
,
where u1, u2 are the eccentric anomalies at the nodes, and
we can explicitly compute tA as a function of a. Thus the above
condition defines a curve in the
![]() plane, as in the
resonant case. Note that this analysis would equally apply even if the
first encounter were with another planet. Figure 2
shows all the possible non-resonant returns to the Earth after the
2027 encounter with
plane, as in the
resonant case. Note that this analysis would equally apply even if the
first encounter were with another planet. Figure 2
shows all the possible non-resonant returns to the Earth after the
2027 encounter with ![]() .
.