

Next: 2.1 Semianalytical theories
Up: Proper elements for Earth
Previous: 1. Introduction
2. Averaging theory for planet crossing orbits
The model employed in this theory is a N-body problem restricted and
circular, that is the asteroid is considered as a massless object and
the Solar system major planets are on circular and coplanar
orbits. Let us describe, for simplicity, the averaging theory for a 3
body problem: Sun-Earth-asteroid.
The Hamiltonian of the system has the form
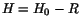 ,
where
,
where
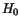 is the 2-body Hamiltonian and
is the 2-body Hamiltonian and 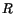 is the perturbing function
is the perturbing function
(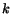 is Gauss' gravitational constant,
is Gauss' gravitational constant,
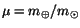 is the ratio of the mass of the Earth and the mass of the Sun,
is the ratio of the mass of the Earth and the mass of the Sun, 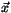 and
and 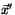 are the positions of the asteroid and the Earth in a
Heliocentric reference frame). In the following we shall exploit the
well known fact that
are the positions of the asteroid and the Earth in a
Heliocentric reference frame). In the following we shall exploit the
well known fact that 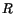 can also be written as a function of
Delaunay variables
can also be written as a function of
Delaunay variables
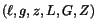 and
and
 ,
of the asteroid and of the Earth, respectively.
,
of the asteroid and of the Earth, respectively.
If the two orbits intersect, then the perturbing function
has a first order polar singularity given by the direct perturbation
term
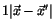 ;
however the integral average of
the perturbing function over the fast angle variables
;
however the integral average of
the perturbing function over the fast angle variables

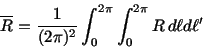 |
(1) |
is a convergent improper integral.
By a classical result the integral average of the
indirect perturbation term
is zero; therefore only the direct perturbations plays a role in this
theory.


Next: 2.1 Semianalytical theories
Up: Proper elements for Earth
Previous: 1. Introduction
G.-F. Gronchi
2000-05-15
![]() ,
where
,
where
![]() is the 2-body Hamiltonian and
is the 2-body Hamiltonian and ![]() is the perturbing function
is the perturbing function
![]() ;
however the integral average of
the perturbing function over the fast angle variables
;
however the integral average of
the perturbing function over the fast angle variables
![]()