When the target is to study the secular evolution of a planet crossing
object, the first order polar singularity of the perturbing function
![]() at the collision points in the phase space results in a second
order polar singularity in its derivatives. Then the integral average
of these derivatives, indicated in equations (2),
is divergent, thus the classical averaging principle does not make
sense.
at the collision points in the phase space results in a second
order polar singularity in its derivatives. Then the integral average
of these derivatives, indicated in equations (2),
is divergent, thus the classical averaging principle does not make
sense.
However, at all the points in the phase space where the asteroid orbit
is not planet crossing the derivatives of the perturbing function are
regular functions, without singularities; there, by the theorem
of differentiation under the integral sign (see [Fleming 1964]),
equations (2) are equivalent to the following
This simple observation can be used to extend the averaging
principle also to planet crossing orbits: we have shown
[Gronchi and Milani 1998] that in the planet crossing case, even if equations
(2) have no sense, it is possible to define piecewise
differentiable solutions of equations (3). The right hand
sides are always defined inside a circular domain in the space
![]() ,
except for the arcs of the node crossing
lines that lie in this domain, where the derivatives of
,
except for the arcs of the node crossing
lines that lie in this domain, where the derivatives of ![]() have a
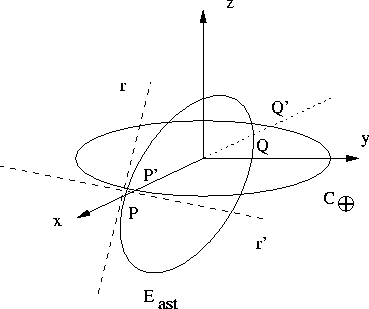
twofold definition (see Figure 1), so that there is
discontinuity of the first kind in the velocity of the solutions at
the node crossing points.
have a
twofold definition (see Figure 1), so that there is
discontinuity of the first kind in the velocity of the solutions at
the node crossing points.
 |
The main idea of the theory is to use a singularity extraction method,
proposed long ago by Kantorovich [Demidovic 1966], to compute the
derivatives; for instance, if the two orbits intersect at the
ascending mutual node and if the differentiation variable is the
eccentricity, so that we have to compute
 |
The choice of this approximate distance allows to extract the
principal part of the singularity from the derivative
![]() and the derivative of the remainder
function
and the derivative of the remainder
function
The first term in the right-hand side of equation (4)
has the same discontinuity properties as the derivative of
![]() ,
but the advantage of this decomposition is that the
computation of
,
but the advantage of this decomposition is that the
computation of
First, the analytical integration of ![]() is performed by
switching to polar coordinates
is performed by
switching to polar coordinates
![]() ;
the result is the sum of
elliptic integrals plus an explicit term under square root:
;
the result is the sum of
elliptic integrals plus an explicit term under square root:
Second, the derivatives (with respect to the orbital elements
![]() )
are applied to this analytical formula; this is an
essential step for the theory, because it allows to write analytical
formulas for the discontinuity of the derivatives of the perturbing
function (see Appendix A). This has an essential role in our
numerical integration scheme (see Section 3), allowing
to ``jump over'' the singularity at the node crossing line.
)
are applied to this analytical formula; this is an
essential step for the theory, because it allows to write analytical
formulas for the discontinuity of the derivatives of the perturbing
function (see Appendix A). This has an essential role in our
numerical integration scheme (see Section 3), allowing
to ``jump over'' the singularity at the node crossing line.
The derivatives, to be used in the right hand side of Hamilton
equations (3), are computed by quadrature of the elliptic
integrals and by explicit computation of the analytical derivatives of
![]() .
This formula is applicable only outside the node
crossing lines, but, unlike the conventional double integral, is
numerically stable on both sides of the node crossing lines.
.
This formula is applicable only outside the node
crossing lines, but, unlike the conventional double integral, is
numerically stable on both sides of the node crossing lines.