


Next: 3.4 Global view of
Up: 3. Results
Previous: 3.2 Resonant and ``pathological''
3.3 Stability
As mentioned above, one of the principal novelties in the present
approach was the derivation of accuracy estimates (standard
deviations and maximum excursions) for every single body included in
our computations. Having all these estimates available, it was
straightforward to perform a simple statistical analysis of the outcome
and to decide on the criteria by which certain bodies qualify for an
extended integration.
In the basic 2 Myr run we found only 6 objects with standard deviation
in proper sine of inclination larger than 0.01; we found a total of
300 of them with
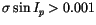 ,
but also 8544 asteroids
with
,
but also 8544 asteroids
with
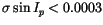 (this value corresponds to
(this value corresponds to 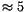 m/s in relative velocity). The situation was, as expected from the
theory, somewhat more complicated for ep: no objects had a standard
deviation larger than 0.1, and only few of them had
m/s in relative velocity). The situation was, as expected from the
theory, somewhat more complicated for ep: no objects had a standard
deviation larger than 0.1, and only few of them had
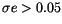 ,
but we found 593 objects with
,
but we found 593 objects with
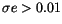 ,
and 2040 of
those with
,
and 2040 of
those with
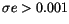 ;
at the same time there are 6687 cases
where
;
at the same time there are 6687 cases
where
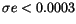 (
(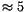 m/s). For more than half of our
sample, more exactly for 5848 asteroids, the two conditions
m/s). For more than half of our
sample, more exactly for 5848 asteroids, the two conditions
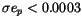 and
and
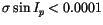 were simultaneously
fulfilled. These results indicate an average improvement in the
accuracy of proper elements by a factor more than 3 with respect to
the previously available elements computed by means of the analytical
theory.
On the other hand we can look at the results in terms of reliability:
in 8009 cases
were simultaneously
fulfilled. These results indicate an average improvement in the
accuracy of proper elements by a factor more than 3 with respect to
the previously available elements computed by means of the analytical
theory.
On the other hand we can look at the results in terms of reliability:
in 8009 cases
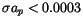 ,
,
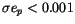 and
and
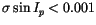 are simultaneously satisfied. This level of
stability was also available for most asteroids from analytical
computations, but we had no way to identify the cases in which this
condition was violated, since tests were performed only on a few tens
of cases.
are simultaneously satisfied. This level of
stability was also available for most asteroids from analytical
computations, but we had no way to identify the cases in which this
condition was violated, since tests were performed only on a few tens
of cases.
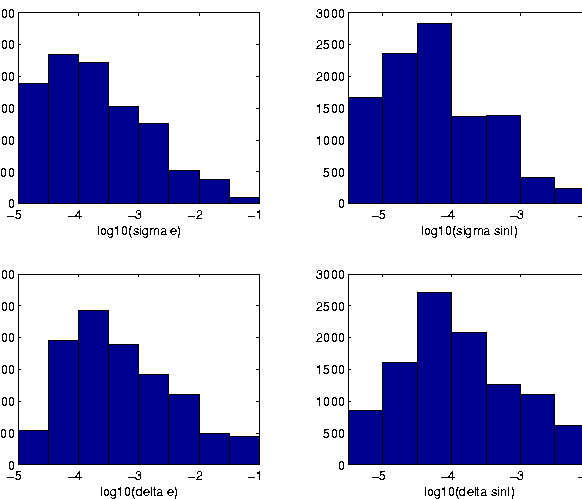
Figure:
Number frequency distributions of standard deviations
(up) and maximum excursions (bottom) of the proper eccentricity (left)
and proper sine of inclination (right), as determined from the
2 Myr integrations.
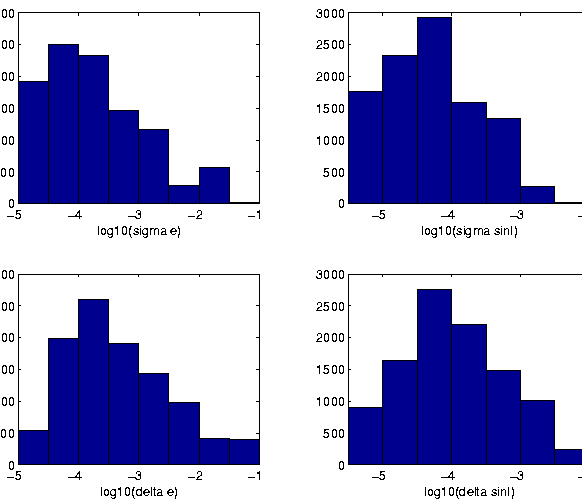 |
On Figure 2 number frequency distributions of the
standard deviations and maximum excursions of the synthetic proper
eccentricity and (sine of) proper inclination are given as derived
from the 2 Myr integrations. The figure illustrates what we have
already stated above, that is, that for the large majority of the
bodies proper eccentricity and inclination are determined with an
exceptionally good accuracy.
Note that the numbers of objects in the bins corresponding to the
largest value of the excursion are one or two order of magnitude
larger than the numbers of bodies in the corresponding bins of the
standard deviation plots. Even for a regular oscillation the maximum
excursions are larger than the standard deviations (by a factor
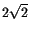 ); however, a much larger ratio between excursion and
standard deviation indicates that the proper value changes abruptly,
but only occasionally and for a comparatively short time.
It is quite obvious that in many troublesome cases an extended
integration might give better and/or more reliable results. For
chaotic objects (see section 3.4), for example, in
particular for the stable-chaos cases, an extended integration,
implying different sampling and filtering, could perhaps provide
results of improved accuracy. For objects affected by secular
resonances with periods up to several Myr, again only an extended
integration can provide enough data for a correct averaging, and so
on. All these arguments had to be considered to select the orbits for
which the integration should have been extended to 10 Myr. We adopted the
following criterium:
); however, a much larger ratio between excursion and
standard deviation indicates that the proper value changes abruptly,
but only occasionally and for a comparatively short time.
It is quite obvious that in many troublesome cases an extended
integration might give better and/or more reliable results. For
chaotic objects (see section 3.4), for example, in
particular for the stable-chaos cases, an extended integration,
implying different sampling and filtering, could perhaps provide
results of improved accuracy. For objects affected by secular
resonances with periods up to several Myr, again only an extended
integration can provide enough data for a correct averaging, and so
on. All these arguments had to be considered to select the orbits for
which the integration should have been extended to 10 Myr. We adopted the
following criterium:
These choices are slightly different from those used above
to assess the quality of the proper elements; in particular, here we
used also the LCE criterion, that is, we included also the chaotic
objects. We found a total of 1860 objects meeting at least one of
these conditions, and thus qualifying for a 10 Myr integration; this
number represents an acceptable compromise between the need for
extending as many orbits as possible and the available computing
power.
The extended integration resulted in 307 ``recovered'' good results,
that is asteroids with
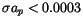 ,
,
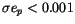 and
and
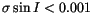 simultaneously satisfied. As already
mentioned, 14 objects became hyperbolic; we found 1347 objects with
simultaneously satisfied. As already
mentioned, 14 objects became hyperbolic; we found 1347 objects with
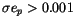 ,
642 objects with
,
642 objects with
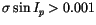 ,
and
475 objects with
,
and
475 objects with
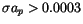 .
.
Figure:
Number frequency distributions of standard deviations (up)
and maximum excursions (bottom) of the proper eccentricity (left) and
proper sine of inclination (right), with data from the joint
catalog. Note an increase of the number of asteroids with large
errors.
 |
Eventually, the final catalog was formed by joining the two outputs,
that is by replacing the 2 Myr output with the 10 Myr one for the
asteroids for which the latter was available. Since in some cases the
instability accumulates with time, this results in an increase of the
number of cases with large instability (compare
Figure 2 with Figure 3, and
Figure 4 with Figure 5). For example out
of 8009 proper elements sets rated as good in the 2 Myr run, 513
actually correspond to the chaotic objects (
TL < 20,000 yr); they
have been included in the extended integration, exhibiting thereafter
an apparent deterioration of the statistics simply because chaotic
diffusion in the proper elements space had more time to act. In other
words, the extended integration revealed a number of asteroids with
poorly determined proper elements, and these results, even if
apparently worse in terms of a simple minded statistics, are in fact
better and more reliable.
Summarizing the final results we report 478 objects with
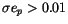 and 2259 with
and 2259 with
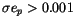 ,
9 with
,
9 with
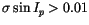 and 650 with
and 650 with
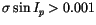 .
For 6382 asteroids we
found
.
For 6382 asteroids we
found
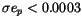 ,
for 6856
,
for 6856
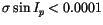 ,
and
5625 fulfilling both conditions. We found in 7804 cases all three
standard deviations being good (
,
and
5625 fulfilling both conditions. We found in 7804 cases all three
standard deviations being good (
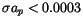 ,
,
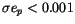 and
and
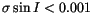 ). In Table 4 we list all the above
quoted, as well as some additional results (for other values of the
standard deviations) on the three sets of data, while in
Figure 3 we show number frequency distributions for
the final joint output (to be compared with Figure 2).
Some questions could arise about the reliability of our estimates of
the accuracy of proper elements for the asteroids whose orbits have
been computed for 2 Myr only. Could some of these turn out to be more
unstable over an extended time span? Out of
). In Table 4 we list all the above
quoted, as well as some additional results (for other values of the
standard deviations) on the three sets of data, while in
Figure 3 we show number frequency distributions for
the final joint output (to be compared with Figure 2).
Some questions could arise about the reliability of our estimates of
the accuracy of proper elements for the asteroids whose orbits have
been computed for 2 Myr only. Could some of these turn out to be more
unstable over an extended time span? Out of
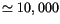 cases, it
would be unwise to make an absolute statement that this could never
happen. However, the orbits selected for the extended integration have
been the ones already showing instability of the proper elements
and/or chaotic behavior, and the others are less likely to become
unstable after having already been regular over 2 Myr. Still, this
cannot be guaranteed.
cases, it
would be unwise to make an absolute statement that this could never
happen. However, the orbits selected for the extended integration have
been the ones already showing instability of the proper elements
and/or chaotic behavior, and the others are less likely to become
unstable after having already been regular over 2 Myr. Still, this
cannot be guaranteed.
Table:
Comparative analysis of the outputs: 2 Myr integration (10256
asteroids), 10 Myr integration (1846) and joint data (10256). The last
row corresponds to
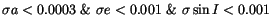 .
.
| Statistics |
|
-2 |
10 |
joint |
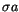 |
> 0.001 |
45 |
131 |
138 |
 |
> 0.0003 |
273 |
475 |
488 |
 |
> 0.0001 |
781 |
823 |
1022 |
 |
> 0.00003 |
1592 |
998 |
1691 |
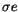 |
> 0.01 |
593 |
472 |
478 |
 |
> 0.003 |
885 |
1002 |
1013 |
 |
> 0.001 |
2040 |
1347 |
2259 |
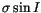 |
> 0.01 |
6 |
7 |
9 |
 |
> 0.003 |
28 |
248 |
252 |
 |
> 0.001 |
300 |
642 |
650 |
 |
> 0.0003 |
1712 |
1101 |
2091 |
| TL |
< 10000 |
499 |
478 |
490 |
 |
< 20000 |
892 |
777 |
789 |
 |
< 50000 |
1617 |
930 |
1603 |
 |
< 100000 |
2216 |
985 |
2220 |
 |
< 200000 |
2755 |
1014 |
2757 |
| |
|
|
|
|
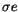 |
< 0.0003 |
6687 |
129 |
6382 |
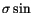 I
I |
< 0.0001 |
7019 |
424 |
6856 |
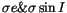 |
|
5848 |
96 |
5625 |
| |
|
|
|
|
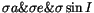 |
|
8009 |
307 |
7804 |
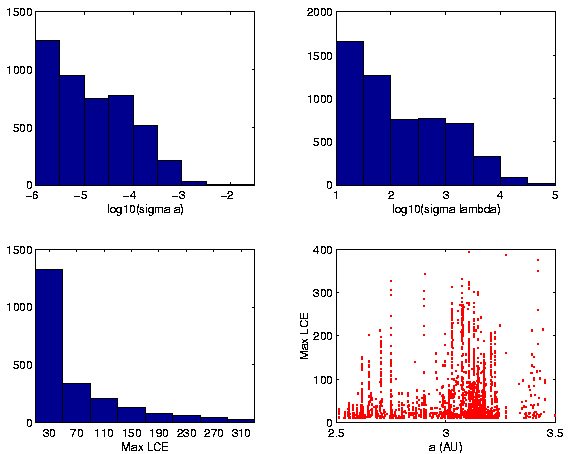
In Figures 4 and 5 we show the number
frequency distributions of the semimajor axes standard deviation, of
the mean longitude differences with respect to the linear fit, and of
the maximum Lyapunov Characteristic Exponents (LCE). In addition,
there are plots of LCE vs. proper semimajor axis to reveal the chaotic
regions in the outer main asteroid belt. The latter plots are similar
to the one produced by Morbidelli and Nesvorný ([1999];
Figure 1), but ours are produced with the initial conditions of real
objects, rather than with fictitious initial conditions on a
grid. It is easy to see that the regions of strongest chaos coincide
with the main mean motion resonances, that the region between 3.0 and
3.2 AU hosts many moderately and strongly chaotic asteroids, and that,
in general, these plots are qualitatively identical with those
obtained in simulations. The largest maximum LCE of
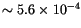 corresponds to
corresponds to
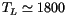 yr. The detailed statistics
of LCE can be found in Table 4.
yr. The detailed statistics
of LCE can be found in Table 4.
Figure:
Upper plots give number frequency distributions of standard
deviations of proper semimajor axis (left) and of the difference in
degrees of the mean longitude with respect to the linear fit (right),
as obtained in the 2 Myr integrations. Lower plots give for the same
integration the number frequency distribution of maximum Lyapunov
Characteristic Exponents (left), and LCE vs. proper semimajor axis
(right).
 |
The chaos in the asteroid outer main belt is due mostly to the mean
motion resonances (including the three-body ones; see Nesvorný and
Morbidelli [1998]), and therefore the chaotic orbits are
characterized by comparatively large irregular oscillations of the
proper semimajor axes. These are quite well known facts, and they are
fully confirmed on Figures 4 and 5, as
well as on Figure 6 showing a clear correlation between
the maximum LCE and the standard deviation of the proper semimajor
axis. In other words, both these quantities are quite sensitive
indicators of chaotic behavior and can be used to detect and measure
it. The statistics of the residuals of the mean longitude with respect
to a linear fit can also be used as a very sensitive indicator of
chaos, although its use is somewhat more difficult, because our
theoretical understanding of its significance is incomplete.
Figure:
The same as Figure 4, but for
the data from the joint catalog.
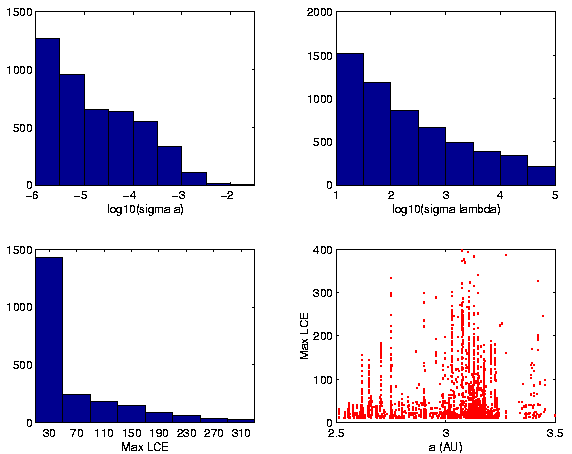 |
The LCE data, as shown in Figures 4 and
5, do not change significantly between the 2 Myr
integration and the 10 Myr one. This was expected, as even the shorter
integration was long enough for a reliable determination of the
maximum LCE for the strongly chaotic orbits with short Lyapunov
times. Still, one can notice in Table 4 that the number of orbits with
TL less than 20,000 yr is slightly decreased in the joint catalog
with respect to the 2 Myr run; this because in the extended integration
the maximum LCE estimate was more accurately determined, especially for
the moderately chaotic orbits. This resulted in somewhat lower
estimates of the maximum LCE in the extended run, but, as a rule, of
the same order of magnitude as that found previously.
Figure:
Maximum LCE and standard deviation of the
proper semimajor axis. A clear correlation between these two
indicators of chaotic motion is apparent. The largest values of
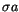 are not shown.
are not shown.
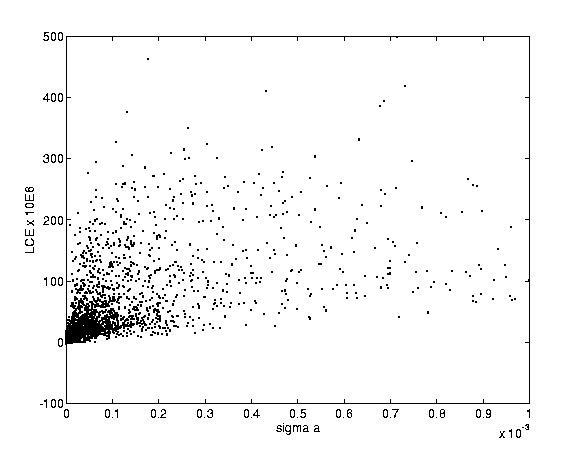 |



Next: 3.4 Global view of
Up: 3. Results
Previous: 3.2 Resonant and ``pathological''
Andrea Milani
2000-10-03




