3. The averaged numerical integration

The numerical method we use to solve Hamilton equations (3) is an implicit Runge-Kutta-Gauss algorithm of order 6, which is also symplectic [Sanz-Serna 1988].

In a previous work we used a simpler algorithm to compute the time evolution of an Earth crossing asteroids without removal of the singularities of collision [Milani and Gronchi 1999], but the procedure was not reliable, depending in an unstable way upon the nodal distance at each Runge-Kutta substep. Thus it was possible to compute proper elements only for one asteroid at a time, and with comparatively frequent human interventions in the computational procedure. To compute proper elements for hundreds of NEA's we need numerically stable algorithms and fully automated, reliable software.

The method of Kantorovich, besides being an essential tool in the theoretical proof of the existence of the generalized solutions, is employed in this work in the numerical integration algorithm when an orbit is very close to a node crossing. This stabilizes the computation even when the nodal distance is small and the averaging integrals are ``almost improper'', that is with very sharp extrema.

  

Figure: Graphical description of the algorithm employed in this numerical integration: it is an implicit Runge-Kutta-Gauss method, symplectic, of order 6. In an integration step, delimited by two consecutive circles, the only points in which the derivatives of $\overline {R}$ are computed are the 3 intermediate points marked with crosses. When the node crossing line is reached, at the end of one integration step, a correction taking into account the explicitly computed jump of the derivatives is added to the right-hand sides of the equations.

However, also in the present algorithm the right-hand side of equations (3) are never computed at the node crossing points, where they are defined in a twofold way. This is possible because the Runge-Kutta-Gauss methods use substeps which include neither the starting point nor the final point of the step being computed. We resort to the following procedure (which had already been used in [Milani and Gronchi 1999]): every time the asteroid orbit is close enough to a node crossing line, a regula falsi method is used to set the second extreme point of the step on that line; as the computation of the right-hand sides is performed only in the intermediate points, the computation at node crossings is avoided.

When the node crossing point is reached within the required precision, the integration needs to restart from there for the next step. In the implicit Runge-Kutta schemes the following step restarts the iterations (to solve the implicit equations) from a first guess, obtained by polynomial extrapolation, of the values used in the previous step. This would fail in this case, because of the discontinuous jump of the right-hand side of (3); we apply to the first guess, extrapolated from values computed before the jump, a correction computed by means of the explicit analytical formula for the jump of the derivatives of $\overline {R}$ (see Appendix).

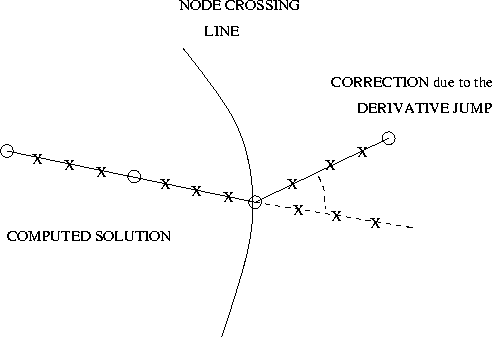
There are a number of technicalities involved in the regula falsi method to arrive at the node crossing line exactly at the end of one integration step. The main problem is that, the right hand side being discontinuous on the node crossing line, the integration steps need to be controlled to be rather shorter than longer than the exact time span to node crossing, to avoid running into the discontinuous behavior. The regula falsi iterations can start only when a change in the sign of the nodal distance takes place between the last intermediate point of the step and the beginning of the next step (with the symbols used in Figure 3, the node crossing line must be between the last cross and the next circle). If a change of sign already occurs in the intermediate points, the stepsize is halved. Even when no change of sign occurs in the current step, an extrapolation algorithm is used to predict whether a node crossing could take place in the next step. For this purpose, the stepsize to crossing is computed in two ways, by regula falsi, that is by a linear extrapolation, and by polynomial extrapolation; the minimum of the two is taken as a prudent estimate of the stepsize to crossing. If the stepsize to crossing is less than the stepsize used in the non crossing portion of the integration, the stepsize of the integration is adjusted to this prediction, to avoid ``overshooting'' of the node crossing line.

A separate regula falsi algorithm is used to compute the value of the orbital elements solution of the averaged equations exactly at the symmetry lines (which are $\omega=0,\pi/2,\pi,3/2 \pi$); the computation of the proper elements requires, at least for the circulation and symmetric libration cases (see Section 5), to compute the solution of the averaged equations between two successive crossings of the symmetry lines. The complete secular evolution is obtained by means of the symmetries $\omega\longmapsto \omega+\pi$ and $\omega\longmapsto -\omega$.

The computation of the proper frequencies requires some additional comment. Let us suppose we have, from the output of the numerical integration of the averaged equations, the times $t_0$ and $t_{\pi/2}$at which $\omega=0$ and $\omega=\pi/2$, respectively, and the corresponding values $\Omega_0$ and $\Omega_{\pi/2}$ of the longitude of the node. The secular frequency of the argument of perihelion is computed taking into account that in this case $\omega$ must be circulating: because of the symmetries, the period of this circulation must be four times the time interval required by an increase by $\pi/2$:

$$g-s=\frac{2\pi}{4(t_{\pi/2}-t_0)}\ .$$

The proper frequency $s$ of the node has to be computed taking into account that the node has a secular precession, but also long periodic oscillations controlled by the argument $2\omega$. The averaged Hamiltonian does not contain $\Omega$, but only the cosine of $2\omega$, thus the perturbative equation of motion for $\Omega$ is

$$\frac{d\Omega}{dt}= -\frac{\partial {\overline R}(2\omega)}{\partial Z}\ ;$$

if $\omega$ is circulating, then it is possible to change (at least locally) independent variable and write the equation directly linking $\Omega$to $\omega$:

$$\frac{d\Omega}{d\omega}= \frac{\partial{\overline R}/\partial{Z}}{\partial{\overline R}/\partial G}=F(2\omega)$$

where the function $F$ only contains $\cos(2\omega)$. By quadrature, the solution for $\Omega$ as a function of $\omega$ is:

$$\Omega(\omega)=\alpha \; \omega + f(\sin(2\omega))$$

and the function $f(\sin(2\omega))$ is zero for $\omega=0,\pi/2$, thus

$$\Omega_{\pi/2}-\Omega_0= \alpha \; \pi/2$$

identifies the secular part of the evolution of $\Omega$, whose frequency can be thus computed simply by

$$s=\frac{\Omega_{\pi/2}-\Omega_0}{t_{\pi/2}-t_0} \ .$$

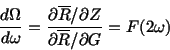
The symmetric libration cases are different in that $\omega$ returns to the same multiple of $\pi/2$ after a time interval $\Delta t$, while in the same time span $\Omega$ has changed by $\Delta \Omega$. Then $g-s$ is not a proper frequency (its secular part is by definition zero), and by arguments similar to the ones above, the libration frequency $lf$ and the secular frequency of the node $s$ can be computed by

$$lf=\pm \frac{2\pi}{2\Delta t}\phantom{=}\phantom{=} s=\frac{\Delta \Omega}{\Delta t}$$

where the sign has to be chosen negative for clockwise libration.

In the asymmetric libration case the procedure to terminate the numerical integration and to compute the proper frequencies would have to be different, but, as discussed in Section 5, this case did not occur in the proper elements catalogs we have computed so far.