3. Algorithm description

Even if it is possible to define a non singular algorithm that computes the averaged solutions of Eqs.(1) just following the steps used in the proof of the existence theorem, we try to exploit the qualitative information, that is the properties of the singular solution appearing in our analytical theory, to define a simpler algorithm. We have used a Runge-Kutta-Gauss method which is symplectic (see Sanz-Serna 1988); this property is useful to maintain the Hamiltonian character of the solutions.

  

Figure 3: the Runge-Kutta-Gauss algorithm computes the values of the derivatives only in non-singular points and as the node crossing line is reached the values of the solution, computed as an analytical function, are modified on the basis of an analytical computation.

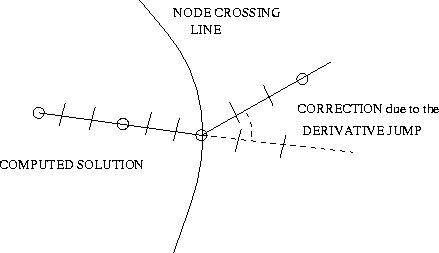
Like all the methods based upon the Gaussian quadrature, the choice of the intermediate nodes does not require to compute the right-hand sides of the equations, that is the derivatives of the averaged Hamiltonian, in the singular points (note that, if we are not on a node crossing line, we can compute the derivatives of $\overline{R}$ as the averaged derivatives of $R$).

This is the main idea of this algorithm: it computes intermediate values of the derivatives between two extreme points and, by successive iterations, tries to reach the singularity in an exact way with a second extreme. This is performed by a control on the nodal distance based upon regula falsi. When we arrive to a node crossing line we continue our extrapolation of the solution as an analytical function, but we add the term that causes the jumps in the derivatives (see Figure 3); the analytical expression of this jump is available from the theory (Gronchi and Milani 1998 and 1999).