4.2 Nonlinear effects due to the propagation

From the formulas of the previous subsection it is clear that both the normal and the covariance matrices contain some coefficient growing quadratically with time; this corresponds to the intuitive notion that the uncertainty, along the $\lambda$ axis, grows linearly with time, and is proportional to the uncertainty in semimajor axis $\sigma_a=\sqrt{\gamma_{11}}$. However, this is true only for infinitesimal $\sigma_a$, because even the 2-body integral flow is nonlinear with respect to the variable a; moreover, this nonlinear effect grows with time, thus no matter how small was $\sigma_a$ at epoch t₀, the value of $\gamma_{66}=\sigma^2_\lambda$ always becomes too large to remain in the quasi-linear region provided the time span $\Delta t$ is long enough. The conditioning number of both the normal and the covariance matrix goes to infinity, at least quadratically with time (even faster for close approaching orbits).

If the normal and covariance matrices are propagated with the formulas given above, and then the ellipsoid of confidence is recomputed for time t with $\Delta t=t-t_0$ large, it is defined by the inequality

$$\begin{eqnarray*}{\displaystyle m \over \displaystyle 2}\;\Delta Q (X)&\simeq& \... ...t \over \displaystyle 2a}\,E_{61}\right]\, \Delta X\leq \sigma^2 \end{eqnarray*}$$

while the image of the confidence ellipsoid for t₀ by means of the integral flow $\Phi_{t_0}^t$ is defined by the inequality

$${\displaystyle m \over \displaystyle 2}\;\Delta Q (X)\simeq \... ..._0 \, \left[\Delta X -\Delta n\Delta t E_6\right]\leq \sigma^2$$

with $\Delta n$ the change in mean motion between the value n(a) for the least squares solution and the value $n(a+\Delta a)$ corresponding to $\Delta X$. If we approximate $\Delta n\Delta t\simeq -(3n/2a)\Delta a\Delta t$ we obtain the previous formula; but for large enough $\Delta n\Delta t$, that is when the along track uncertainty is large, this approximation fails.

The size of this effect can be estimated in a simple way by using a one-dimensional argument, that is by neglecting all the correlations of the longitude with the other elements; a more complete and rigorous argument could be used, but it would not change the conclusions. The squared marginal uncertainty in $\lambda$, when computed from the covariance matrix at time t, is

$$\sigma^2_\lambda(t)= \sigma^2_\lambda(t_0) +\left({\displaystyle 3n\Delta t \over \displaystyle 2a}\,\sigma_a\right)^2\ ;$$

while the same uncertainty, computed from the confidence ellipsoid at time t₀, is

$$\sigma^2_\lambda(t)= \sigma^2_\lambda(t_0) +\left({\displaystyle \Delta n\Delta t \over \displaystyle n}\, \sigma_a\right)^2$$

which can be very different. Note that the function n(a) is convex:

$${\displaystyle \Delta n \over \displaystyle n}= -{\displaysty... ...playstyle \Delta a \over \displaystyle a}\right)^2 + \ldots\ ,$$

that is, the linear estimate of the uncertainty is more pessimistic, with respect to the nonlinear one computed from the covariance at t₀, on the side $\Delta a >0$, more optimistic on the other side.

It follows that the semi-linear confidence boundary, introduced in Section 3.3, needs to be computed from the covariance matrix relative to the orbital elements at a time close to the real observations; whenever the confidence prediction region is large, e.g. tens of degrees as in the examples of Figures 1-8, the computation from the covariance matrix of the elements ``now'', that is close to the time of the planned recovery observation, could fail by a large amount.

  

Figure: Simulated precovery of the asteroid 1994 CD2, at the time of 1976 GA2, with which it has been identified [Sansaturio et al. 1996]. The continuous faint line is the confidence boundary for $\sigma =1$ computed, starting from the 1994 covariance matrix, with the 2-body approximation defined in the text; the actual precovery observation of 1976 GA2 is marked with cross and circle (a copy displaced by 360 degrees on the left gives a better agreement). The crosses are the results of the same computation, starting from the covariance matrix propagated to 1976. Most of the crosses do not appear in the plot, because the confidence boundary computed with the wrong approximation contains mostly hyperbolic orbits; this is not surprising, considering that $\sigma _\lambda = 278$degrees!

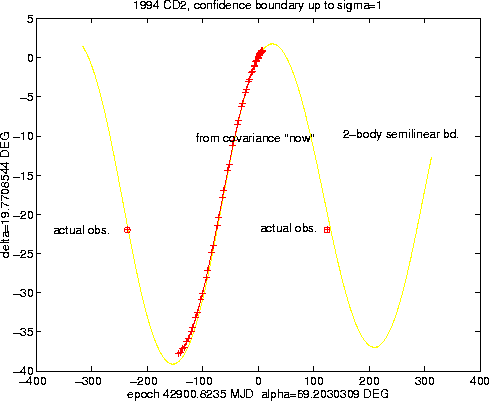This conclusion has some embarrassing implications. The problem should be considered from the point of view of some orbit computing centre (or consortium), which is providing to the observers a service of prediction of the asteroid positions on the celestial sphere. As should be clear from the discussion presented so far, to provide one prediction is not enough, at least not for the totally lost asteroids, because it does make possible neither to plan for a recovery with significant probabilities of success, nor to identify a serendipitous recovery. To provide a confidence ellipse significantly increases the efficiency, provided the semiaxes of the ellipse are not too big (say, less than one degree of arc). For such comparatively small uncertainties, also the simple approximation to the line of variations obtained by changing only the asteroid mean longitude is often good enough.

  

Figure: For 9076 PLS, the semi-linear confidence boundary for $\sigma =1$ is computed from the covariance matrix ``then'', that is at the time of the observations in 1960, and from the covariance matrix ``now'', that is at a time very close to the prediction time. The first computation successfully predicts where the asteroid has been recovered (as 1993 QB5), while the second one fails. The failure is even more spectacular than it is apparent from this plot, because our computations exclude the hyperbolic orbits, which would further extend the confidence boundary computed from ``now'' on the left of the figure. The 2-body approximate computation, as proposed in this Section, is the line close to the n-body approximation; it is not very accurate but still correctly predicts the recovery observation. The linear approximation of the confidence ellipse is also shown.

When the semiaxes of the confidence ellipse reach several degrees, what would be required is a computation of the semi-linear confidence boundary, as defined in Section 3.3; however, this definition depends upon the time t₀ for which the covariance matrix has been computed. If the covariance matrix is computed for the discovery epoch, as suggested in [Muinonen et al. 1994], and accurately stored, then the prediction of the confidence boundary restarting from $\Gamma_0, C_0$ can be accurate as shown in the examples of the Figures 1-2 and 4-5. This requires, however, the computation of a number of orbits for a long time span, as long as the time interval for which the asteroid has been lost. If on the contrary the catalogue of covariance and normal matrices is kept up to date, the predictions from the confidence ellipsoid of the elements ``now'' will be computationally very efficient, but the computation of the confidence prediction region is not reliable.

Two solutions can be offered to this dilemma. The first one is to set up an algorithm (and software system) which is very efficient in computing accurate orbits. Appendix A describes what we have achieved with our software system OrbFit, which is indeed efficient enough to generate all the computations and the figures of this paper with a personal computer.

The second solution is to use a less accurate approximation, with negligible computational cost. Since, as pointed out above, the nonlinearity of the integral flow is already contained in the 2-body problem, we have experimented with a 2-body approximation to compute the effect of the nonlinearity of the confidence region propagation. The algorithm is as follows: an accurate orbit, and observation prediction Y₀, is computed for the least square solution. Then the same prediction is computed by means of a 2-body propagation, let this approximation be Y₂. The semi-linear confidence boundary $K_N(\sigma)$ is computed as a sequence of points (typically a few tens to a few hundreds) Y_i, all of them in the 2-body approximation; then the prediction of $K_N(\sigma)$ is approximated by Y_i-Y₂+Y₀.

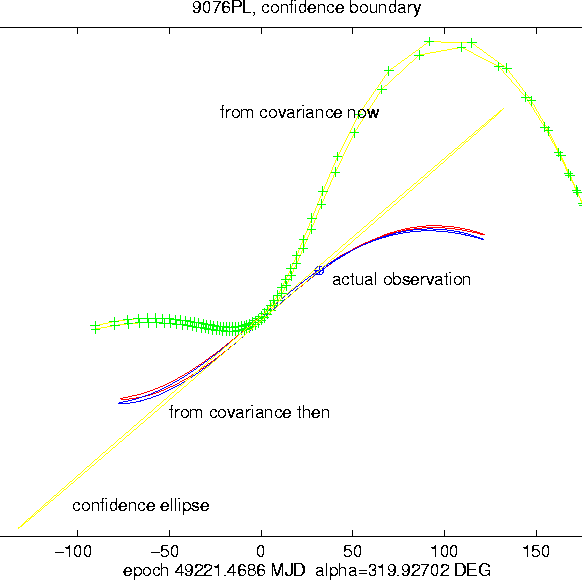
This 2-body approximation can not be used in all cases; it is bound to fail whenever there are close approaches (as in the case of Figure 8) and/or resonant perturbations. It is also often not accurate enough for Earth-crossing asteroids, even in absence of very close approaches, because to predict the observations during a comparatively close passage the position in the sky of the asteroid has to be known with significantly better precision than it is the case for a main belt object. However, for main belt asteroid this 2-body nonlinear approximation is often of satisfactory accuracy, as in the cases shown in the Figures 11-12.

As an example we use the case already presented in Figure 4, namely 9076 PLS, a long lost asteroid which was recovered as 1993 QB5, and only later identified. The covariance matrix at the time of discovery, in 1960, had a conditioning number of $3.7\times 10^9$ and a marginal uncertainty for $\lambda$ of $\sigma_\lambda=\sqrt{\gamma_{66}}=2.3$ (in degrees). The covariance matrix, propagated with a full n-body integration (as described in Section 2.4) to the recovery epoch in 1993, has a conditioning number of $2.5\times 10^{14}$, very hard to handle numerically with the usual rounding off level of $1/5\times 10^{15}$, and $\sigma_\lambda= 62.1$ degrees. Already at the $\sigma =1$ level, as shown in Figure 12, the nonlinear contribution to the propagation of the confidence ellipsoid is so large, that the semi-linear confidence boundary is totally different when computed from the covariance matrix ``now''. In this case, the semi-linear confidence boundary computed from covariance ``now'' fails, by a large amount, to enclose the actual recovery observation. This example has some strange properties: the linear approximation of the confidence ellipse, even if the overall shape has nothing to do with the confidence prediction region, does include the recovery observation; the 2-body approximation proposed above is also successful. However, this happens in this case, in which the recovery observation is closer to the least square prediction than one would ordinary expect by chance, at about $\sigma=1/3$.

It is also worth noting that the confidence region is almost always, for long lost main belt asteroids, a very narrow strip along the variation line (to be computed as described in Section 3.3), with a width which is often a few arc seconds. For the purpose of recovery, an error in the computation of the confidence boundary by a few arc minutes is uninfluential, since anyway the field of view of the telescopes used for the search is not likely to be a few arc seconds! As an example, in the case discussed in the Figures 2-3, the error in prediction, which is many degrees with the linear formalism (Figure 3), reduces to about 50 arc minutes with the 2-body approximation.

With all this, the problem of devising an efficient strategy to provide confidence boundary computations for a large catalogue of asteroids is not easy to solve. Some hints to a possible solution are given in Section 6.