


Next: 3. Results
Up: 2. The filtering procedure
Previous: 2.2 The checking algorithm
2.3 The confirmation algorithm
The third step is the application of the classical differential
correction procedure to all the orbit-attributable pairs selected by
the second stage. We try to fit (in the least squares sense) an orbit
to the observations of both arcs, by using as first guess the orbit of
the first arc. For this we use the OrbFit software which has
been thoroughly optimized, but still this is the most CPU time
consuming part of the attributions work; for the May 2000 update we have used
more than 100 hours of CPU. As it is clear from
Table 1, this is mostly due to the short arc orbits
for which the second filter is not selective enough.
Figure:
Histogram of the number of attributions,
submitted by us and published by the MPC, as a function of the
weighted RMS of the residuals of the least squares fit for the
observations of both arcs.
Figure:
Histogram of the number of attributions,
submitted by us and published by the MPC, as a function of the
weighted RMS of the residuals of the attributed observations only.
 |
The differential correction procedure we use has three features which
are relevant for this paper. First, the differential correction is
iterated until convergence is achieved; this feature is especially important
because fitting an attribution to a single opposition orbit may need a
comparatively large correction, well outside of the linearity region.
For controlling the convergence of the iterations, we use as
termination condition
where the norm
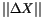 of the last correction to the orbital
elements is defined by means of C, the normal matrix in the elements
space, in such a way that a correction has a small norm if it is much
less than the corresponding uncertainty.
Second, the algorithm normally used to fit asteroid orbits to the
observations, e.g., to prepare the orbit catalog we use as starting
point, includes an automated outliers rejection procedure
[Carpino et al., 2000]. However, we disable the outliers rejection for the
attribution confirmation procedure. The outliers which have already
been rejected during the fit of the first arc remain rejected, but no
others are added, in particular no rejections are performed among the
observations of the second arc. This way of acting is in general appropriate,
although once an attribution is accepted it is sometimes possible to
further improve the fit by outliers rejection. On the other hand, if we
were to perform outliers rejection for attributions which are still
dubious, we would often end up rejecting proportionally too many of
the few observations of the second arc, even rejecting the second arc
entirely and going back to the first arc orbit.
Third, the differential correction algorithm we use minimizes a
weighted RMS of the residuals:
of the last correction to the orbital
elements is defined by means of C, the normal matrix in the elements
space, in such a way that a correction has a small norm if it is much
less than the corresponding uncertainty.
Second, the algorithm normally used to fit asteroid orbits to the
observations, e.g., to prepare the orbit catalog we use as starting
point, includes an automated outliers rejection procedure
[Carpino et al., 2000]. However, we disable the outliers rejection for the
attribution confirmation procedure. The outliers which have already
been rejected during the fit of the first arc remain rejected, but no
others are added, in particular no rejections are performed among the
observations of the second arc. This way of acting is in general appropriate,
although once an attribution is accepted it is sometimes possible to
further improve the fit by outliers rejection. On the other hand, if we
were to perform outliers rejection for attributions which are still
dubious, we would often end up rejecting proportionally too many of
the few observations of the second arc, even rejecting the second arc
entirely and going back to the first arc orbit.
Third, the differential correction algorithm we use minimizes a
weighted RMS of the residuals:
where m/2 is the number of observations, 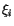 are the residuals,
and the weight wi is computed for each observation as a function of
the performance of the same observatory over a time span long enough
to allow for statistical analysis [Carpino et al., 2000].
An orbit-attribution pair is considered passed by the third stage
filter when the weighted RMS of the residuals
are the residuals,
and the weight wi is computed for each observation as a function of
the performance of the same observatory over a time span long enough
to allow for statistical analysis [Carpino et al., 2000].
An orbit-attribution pair is considered passed by the third stage
filter when the weighted RMS of the residuals 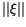 is below some
critical value
is below some
critical value 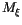 .
For a successful orbit determination, we
expect that
.
For a successful orbit determination, we
expect that
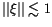 ,
but this is true only for good
orbits and after outlier rejection. Thus, for the attribution
confirmation procedure, a somewhat higher value is acceptable. In
Figure 2 we can see that most of the attributions
already accepted by the MPC have
,
but this is true only for good
orbits and after outlier rejection. Thus, for the attribution
confirmation procedure, a somewhat higher value is acceptable. In
Figure 2 we can see that most of the attributions
already accepted by the MPC have 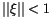 ,
but a fraction have a
somewhat higher value. For the first few months of operations, we
were using
,
but a fraction have a
somewhat higher value. For the first few months of operations, we
were using 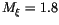 .
If we had used
.
If we had used 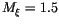 ,
we would have lost
only 2 published attributions; thus we later changed the control value
to
,
we would have lost
only 2 published attributions; thus we later changed the control value
to 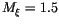 .
The fraction of pairs passing the third checking stage, that is with
a meaningful least squares fit, is small, especially for short arc
orbits. Nevertheless, it is not the case that all of them correspond
to real identifications, and other parameters have to be analyzed to
assess the quality of the fit. Another interesting indicator is
.
The fraction of pairs passing the third checking stage, that is with
a meaningful least squares fit, is small, especially for short arc
orbits. Nevertheless, it is not the case that all of them correspond
to real identifications, and other parameters have to be analyzed to
assess the quality of the fit. Another interesting indicator is
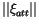 ,
the weighted RMS of the residuals of the attributed
observations only, since the RMS of all the residuals could be
dominated by the residuals of the first arc, especially when it has a
much larger number of observations. We have been using a control
,
the weighted RMS of the residuals of the attributed
observations only, since the RMS of all the residuals could be
dominated by the residuals of the first arc, especially when it has a
much larger number of observations. We have been using a control
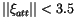 ;
as it is shown in Figure 3, we
could have used
;
as it is shown in Figure 3, we
could have used
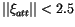 without a significant loss of
attributions. Indeed, for the April 2000 update, the number of
pairs passing the third filtering stage, as shown in
Table 1, was obtained by using the controls
without a significant loss of
attributions. Indeed, for the April 2000 update, the number of
pairs passing the third filtering stage, as shown in
Table 1, was obtained by using the controls
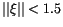 and
and
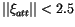 .
.
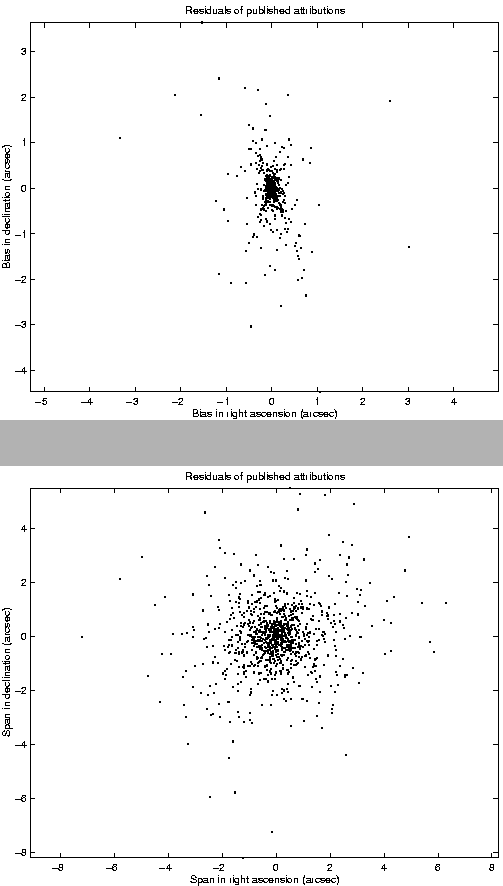
Figure:
Biases of the attributions,
submitted by us and published by the MPC
Figure:
Spans of the attributions,
submitted by us and published by the MPC
 |
Another useful criterion is the detection of signatures in the
residuals for the attributed observations. Since they belong to a
short arc, a simple linear fit to the residuals in both 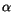 and
and
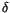 as functions of time gives enough information in most cases.
Separately for right ascension and for declination we compute the
bias, which is the value of the best fitting line at the central time
tm of the attributed arc, and the span, which is the
difference between the values of the best fitting line at the
beginning and at the end times of the same arc.
Figures 4 and 5 show the values of such
quantities for the attributions submitted by us and published by the
MPC. From these figures it is apparent that an additional control,
based upon these values, could be used. Starting from May 2000, we are
using such an additional control based upon bias and span to select
the attributions to be submitted. Let the biases be
as functions of time gives enough information in most cases.
Separately for right ascension and for declination we compute the
bias, which is the value of the best fitting line at the central time
tm of the attributed arc, and the span, which is the
difference between the values of the best fitting line at the
beginning and at the end times of the same arc.
Figures 4 and 5 show the values of such
quantities for the attributions submitted by us and published by the
MPC. From these figures it is apparent that an additional control,
based upon these values, could be used. Starting from May 2000, we are
using such an additional control based upon bias and span to select
the attributions to be submitted. Let the biases be 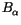 and
and
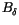 ,
the spans be
,
the spans be 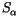 and
and 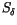 ;
we require
;
we require
for multiple night attributions, and
for one night stands with more than 2 observations; the span has to be
less than 1.6 arcsec for one night stands with only 2 observations.
All these limit values have been empirically determined from experience.



Next: 3. Results
Up: 2. The filtering procedure
Previous: 2.2 The checking algorithm
Andrea Milani
2001-12-31


