The asteroid 1999 AN was discovered by the LINEAR telescope on
13 January 1999. The discovery was somewhat unusual in that the
declination was 
. We checked for possible prediscovery
observations in the archives made available by the Minor Planet
Center, and found none; this is not surprising, given that this
asteroid is typically visible in a portion of the sky which has been
very little surveyed in the past. The asteroid was observed until 20
February: afterwards the angular distance from the sun became
.
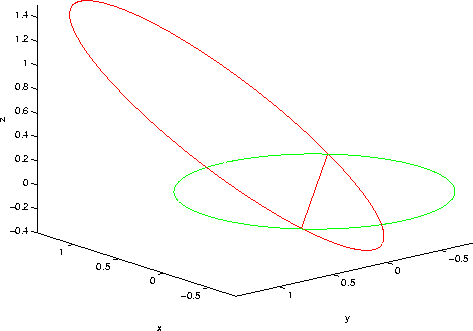
Figure 1: The orbit of 1999 AN and the orbit of
the Earth, in a reference system with the z axis normal to ecliptic
plane, in which the Earth's orbit lies, and the x axis towards the
point. The line of intersection of the two orbital planes is
also drawn. The nodes are both very close to the orbit of the
Earth. This results in two periods of the year when close approaches
are possible, in August and in February.
The nominal orbit published by the online information service
NEODyS[1], that is the solution of the least squares fit to
94 observations (with one outlier removed, RMS of the residuals 0.59
arc-sec), is as follows: a=1.458432 AU, e=0.562093,
, 
,
, 
, for epoch 
. The unique feature of this orbit is shown in
Figure 1: both its intersections with the ecliptic
plane, the nodes, are very close to the Earth's orbit. The ascending
node is only 0.00025 AU closer to the Sun than a point where the
Earth is in early August; the descending node is 0.00478 AU inward
from a position of the Earth in early February. This means that,
whenever the asteroid and the Earth are in phase at each node, close
approaches are possible. Indeed a close approach is possible in August
2027.
To analyse the 2027 encounter, we need to consider not only the
nominal solution, but also all the solutions compatible with the
observations, that is those resulting in residuals which are not much larger
than the ones of the nominal orbit. The region of
these compatible solutions can be approximated by an ellipsoid of
confidence, which can be computed according to the standard theory of
normal and covariance matrices. In the notation of [2], the
confidence ellipsoid corresponding to a 
value up to 3
contains solutions with RMS of the residuals up to 0.63 arc-sec.
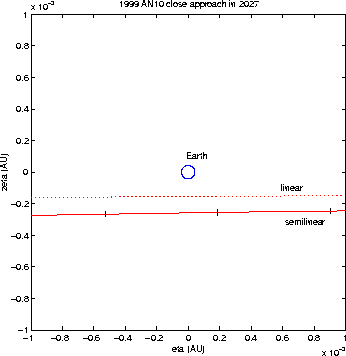
Figure 2: The close approach of August 2027, with its
uncertainty as projected on the Modified Target Plane. The prediction
according to the linear theory would allow for an approach closer than
the one allowed by the more accurate semi-linear theory. In any case,
the Earth (shown to scale) is not at risk. The crosses mark the
alternate orbits computed at a separation of 
along the variation axis.
The nominal solution undergoes a close approach in August 2027 with a
minimum distance from Earth's center of 0.0257 AU. The plane normal
to the geocentric velocity at closest approach is the Modified Target
Plane (MTP) [3]. The hypothetical objects filling the
confidence region evolve along a bundle of orbits; their intersections
with the MTP define the confidence region of the encounter. If the
Earth is not touched by this confidence region, then a collision
cannot occur at that encounter unless the RMS of the observational
errors is significantly larger than the minimum. The boundary of the
confidence region on the MTP can be approximated by the linear
confidence ellipse [4]; however, in cases where the
nominal solution is far from the closest possible approach, the linear
approximation may prove unreliable and the semi-linear method
described in [3] should be used. Figure 2
shows the MTP of the 2027 encounter, with the Earth and the nearby
portions of the linear and semi-linear confidence boundaries. The
confidence regions are very thin, the width being only 
km:
they can be represented as lines in the plot. The confidence region is
much longer than the portion shown, indeed it extends up to 0.21 AU
in both directions (for 
). Thus the occurrence of a very
close approach is not very likely: the true orbit could be anywhere
along a very long line, including long stretches corresponding to very
shallow encounters.
There is no such thing as a unique probability of an event involving
an orbit obtained by a least squares fit; the probability depends upon
assumptions on the statistical distribution of the observational
errors. There are, however, mathematically rigorous methods to deduce
a probability for an event given a hypothesis on the error
statistics. As an example, if the errors were normally distributed
with zero mean and variance of 
arc-sec 
, then the
probability of a 2027 close approach within the distance of the Moon
would be 
. Such a model for observational errors is
questionable, because it underestimates the effect of correlations,
and it assumes an unrealistically low occurrence of large errors. To
compensate for this, we prefer to use a uniform probability density
along the line of variation for ; in the example above,
this would result in a probability of 
. As this example shows,
the values obtained by different statistical error models are
different, and the selection of the appropriate model is not a simple
issue; in the following we shall use the uniform distribution
assumption.
In conclusion, the August 2027 encounter could be a very shallow approach, or could be, with a low, non-negligible probability, very close, but in any case cannot result in an impact. The case for a possible dangerous encounter, however, is not closed after 2027; indeed, it is just opened.