The possibility of a resonant return of an asteroid involved in a
close approach was proposed by B. Marsden [5]. This
idea did not receive the attention it deserved. Marsden applied this
idea only to a hypothetical case, namely the asteroid 1997 XF 
in the assumption that the 1990 precovery observations had not been
discovered. In that hypothetical case there are indeed more than 20
different solutions leading to a return after injection by the 2028
close approach into a resonance with the Earth. The real 1997
XF , with the orbit determined by using all the available
observations, is only mildly perturbed by the 2028 encounter
[3], and cannot have a resonant return.
We can formulate the basic theory of resonant returns as follows. When
an asteroid undergoes a close approach in the future, several decades
after the last available observation, the confidence region on the MTP
is thin (with a width much less than the diameter of the Earth) and
very long, as in Figure 2; thus it is enough to perform
the analysis on the line of variations, which is essentially the long
axis of the confidence region (for a precise definition, see
[3]). The alternate solutions along this line undergo
different degrees of perturbations, as a result of the close
approach. The values of the elements after the encounter describe a
curve in the orbital elements space, e.g. in the (a,e) plane; an
idea of the shape of such curves can be obtained by using Öpik's
approximation, which is essentially a piecewise two body solution, and
is reasonably accurate for encounters with a high relative velocity
[6]. It turns out that these curves are almost closed,
that is they go back to nearly the unperturbed values when the
encounter is shallow, on both extremes of the variations line. In
particular a minimum value 
of the post encounter semimajor
axis a results from a close approach such that the asteroid is
slightly early for the encounter with the Earth, a maximum 
from an orbit which is late [7]. Let 
and
be the corresponding minimum and maximum orbital
periods. Then every rational number in the interval between
and corresponds to at least two resonant returns; if the
period P=h/k years with h,k integers, then after h years the
asteroid has completed k orbits, the Earth has completed h orbits,
and both return to nearly the same position as they were at the
previous encounter. Because the curve in the plane (P,e) is nearly
closed, the lines P=h/k in general cross it an even number of
times. As an example, 1999 AN 
can have several different 7/4
resonant returns in 2034, resulting in an approach potentially closer
than the one in 2027, down to 
AU.
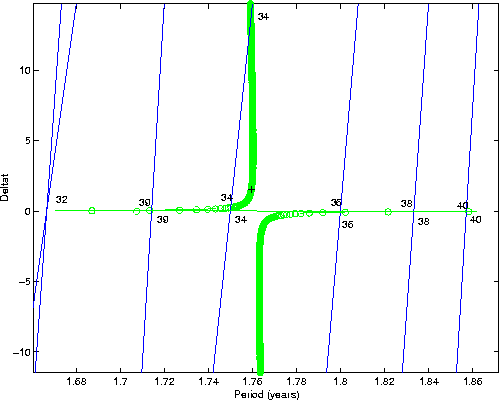
Figure 3: Resonant returns of 1999 AN after the
2027 encounter, taking place until August 2040. The circles represent
alternate solutions along the variations line for the
asteroid orbit. The solid line represents other solutions in the
region of highest stretching. The resonant returns are the
intersections between the straight lines and the line of variations, all
labeled with the year (after 2000) in which the return takes place.
The above theory is still too simple, however, because two further
elements have to be taken into account. The first one is that the
amount of time by which the first encounter has been missed needs to
be recovered to make the second encounter a close approach. As an
example, let us take the 2027 encounter of 1999 AN . If 
is the amount of time by which the asteroid is early for the
encounter with the Earth in August 2027, the condition to be satisfied
for a resonant return at the minimum distance is 
,
where and P are in years. Thus the resonant returns are
described, in the 
plane, by lines which are somewhat
slanted with respect the P=h/k lines. Figure 3
depicts these resonant lines for 
, that is for returns
taking place until August 2040. Where these resonance lines intersect
the line of variations, one finds a resonant return leading to a close
approach. In the figure the line of variation has been traced by using
the multiple solutions algorithm of [2, Sec. 5,]. We have
used solutions equally spaced along the 
axis between
-3 and +3; we have added a denser sampling of solutions along the
axis in the region near the 2027 closest approach. The
intersections with the resonant lines can be easily counted from the
figure; the resonances not touching the line of variations cannot
result in deep encounters, e.g. the P=5/3 resonance can only result
in an approach at 0.07 AU in 2032.
The other element to be taken into account is the so called Minimum
Orbital Intersection Distance (MOID), the minimum distance between the
two osculating ellipses representing the orbit of the Earth and of the
asteroid. Even if the asteroid were exactly on time at the rendezvous
with the Earth, the unperturbed close approach distance cannot be less
than the MOID. In the case of 1997 XF , within a few decades
after the 2028 encounter the MOID becomes large enough to make the
most dangerous encounters impossible. Thus in the hypothetical case
without 1990 precovery only 11 resonances have to be taken into
account to assess the risk of resonant return; for the real case,
there is no resonance with low enough h. For 1999 AN , there
are in fact two local MOID's, one per node; each is 
times the minimum of distance at the respective node. If the MOID was
to remain small forever, since every real number P is approximated
arbitrarily well by a rational number h/k a resonant return after
h years would be always possible.
What is the evolution in time of the local MOID's of 1999 AN ?
It is not enough to compute the evolution of the MOID's along the
nominal solution, because the close approaches can change them: in
particular, an encounter near the ascending node (in August) can
reduce the distance at the descending node, and make possible a closer
approach at the descending node (in February). We have asked
G.F. Gronchi to compute the evolution of the mean orbital elements,
`averaged' in the sense of [8], [9],
[10] in a way accounting also for the secular effects of
the close approaches. The answer is that 1999 AN will continue
to have a very low distance at both nodes, until the crossing at the
descending node, which should take place `on average' in 2633, and
for a few decades later. Thus it is simply not possible to perform
close approach analysis, in the sense of [3], for all
possible resonant returns: there are hundreds of them.