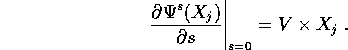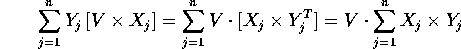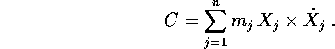



Next: 6.5 SISTEMI HAMILTONIANI
Up: 6 SISTEMI CONSERVATIVI: PIÙ
Previous: 6.3 VINCOLI E COORDINATE
Sommario Ad ogni simmetria della funzione di Lagrange corrisponde un
integrale primo, che può essere calcolato esplicitamente in termini
di momenti e derivate del gruppo di simmetrie. Questo generalizza il
caso delle variabili cicliche. Nei sistemi composti da n corpi
puntiformi, che interagiscono solo tramite forze centrali, le isometrie
sono simmetrie e conducono agli integrali della quantità di moto e
del momento angolare.
Definizione:
-
- si chiama
gruppo ad un parametro di diffeomorfismi una curva di
diffeomorfismi di W: cioè per ogni
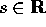

è un diffeomorfismo; inoltre
la somma del parametro s corrisponde alla
composizione dei diffeomorfismi:

Ne segue che 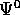 è l'identità su W, e che
è l'identità su W, e che
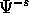 è l'inverso di
è l'inverso di 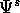 .
.
Le condizioni di regolarità richieste sono le seguenti:
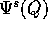 deve avere continue non solo le derivate rispetto
a t e alle coordinate di Q, ma anche quelle miste
deve avere continue non solo le derivate rispetto
a t e alle coordinate di Q, ma anche quelle miste
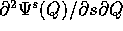 .
.
L'applicazione tra il gruppo additivo 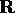 ed il gruppo
dei diffeomorfismi è un omomorfismo di gruppi.
ed il gruppo
dei diffeomorfismi è un omomorfismo di gruppi.
Esempio:
Definizione:
Teorema di Noether :
Se la lagrangiana 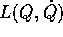 ha un gruppo ad un parametro di
simmetrie
ha un gruppo ad un parametro di
simmetrie 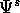 , allora ha un integrale primo con la
seguente espressione:
, allora ha un integrale primo con la
seguente espressione:
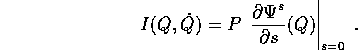
Dimostrazione:
-
-
Calcoliamo l'incremento della lagrangiana lungo le curve
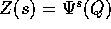 ,
usando lo sviluppo di Taylor in s=0:
,
usando lo sviluppo di Taylor in s=0:
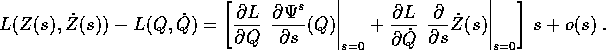
Poiché questo incremento deve essere zero identicamente
rispetto ad s, il termine del primo ordine si annulla:
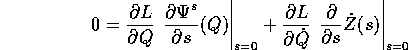
Ora sfruttando il fatto che 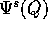 ha derivate miste
continue, possiamo scambiare l'ordine delle due derivate
rispetto ad s e rispetto a t:
ha derivate miste
continue, possiamo scambiare l'ordine delle due derivate
rispetto ad s e rispetto a t:
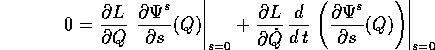
La definizione dei momenti P (trasformata di Legendre
inversa) e le equazioni di Lagrange consentono
di sostituire alle derivate parziali della lagrangiana:
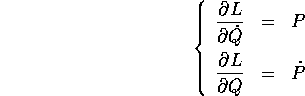
e inserendo queste relazioni nell'equazione precedente:
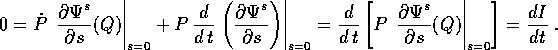
C.D.D.Problema
Dato un pendolo doppio piano in moto libero, trovare
una simmetria che definisca un integrale primo. Trovare un
sistema di coordinate in cui ci sia una variabile ciclica, e
quindi integrare il sistema per quadrature.
Suggerimento: Se i due pendoli ruotano simultaneamente dello stesso
angolo, l'energia cinetica non cambia.
Consideriamo un sistema di n
corpi puntiformi
con coordinate 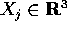 e masse
e masse 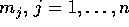 ; indicheremo con X il vettore di
; indicheremo con X il vettore di 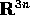 formato
giuntando gli
formato
giuntando gli 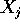 . L'energia cinetica è
. L'energia cinetica è
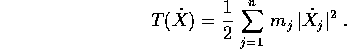
Supponiamo ora che questi corpi interagiscano tra loro due a
due, con una
forza centrale con energie potenziali 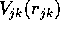 , dove
, dove
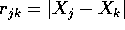 è la distanza dei due. Inoltre supponiamo
che valga la legge di azione e reazione , per cui
la forza esercitata da
è la distanza dei due. Inoltre supponiamo
che valga la legge di azione e reazione , per cui
la forza esercitata da 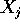 su
su 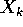 è uguale e contraria
a quella esercitata da
è uguale e contraria
a quella esercitata da 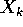 su
su 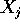 ; questo comporta che
; questo comporta che
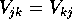 .
.
La legge di azione e reazione così enunciata vale perché i
corpi sono supposti in moto libero; la presenza di reazioni vincolari
renderebbe la formulazione di questa legge più complicata.
Allora esiste un'energia potenziale `totale''
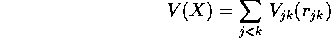
in cui la somma si estende alle coppie non ordinate, in modo
che non ci siano duplicazioni. La lagrangiana
di un tale sistema di n corpi è quindi
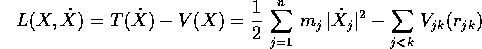
e le equazioni di Lagrange rispettano il
principio di sovrapposizione , per cui
la forza risultante che agisce su di un corpo è la somma
vettoriale di quelle esercitate da tutti gli altri corpi:
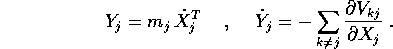
Questo problema, e le equazioni qua sopra, si designano con il nome di
problema degli n corpi . Per applicare il teorema di Noether e
trovare degli integrali primi, basta considerare che l'energia
cinetica dipende solo dalla lunghezza delle velocità, mentre
l'energia potenziale dipende solo dalle distanze. Perciò ogni
trasformazione dello spazio 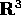 che sia un'isometria ,
cioè che conservi le lunghezze, applicata simultaneamente a tutti
gli n corpi, lascia la lagrangiana del problema degli n corpi
invariante. Ogni sottogruppo ad un parametro del gruppo delle
isometrie darà quindi luogo ad un integrale primo.
che sia un'isometria ,
cioè che conservi le lunghezze, applicata simultaneamente a tutti
gli n corpi, lascia la lagrangiana del problema degli n corpi
invariante. Ogni sottogruppo ad un parametro del gruppo delle
isometrie darà quindi luogo ad un integrale primo.
Infatti consideriamo un'isometria di 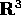 : per il teorema delle
rotazioni di Eulero , si potrà sempre esprimere come
composizione di una rotazione
: per il teorema delle
rotazioni di Eulero , si potrà sempre esprimere come
composizione di una rotazione 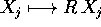 e di una
traslazione
e di una
traslazione 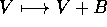 , cioè nella forma
, cioè nella forma
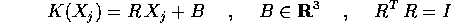
Se si applica la stessa isometria (indipendente dal
tempo) a tutte le posizioni 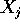 , la lunghezza delle
velocità non cambia:
, la lunghezza delle
velocità non cambia:
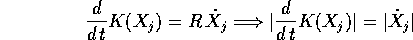
e le distanze neppure:
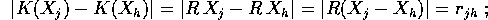
usando la notazione K(X) per indicare il vettore di
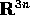 formato giuntando i
formato giuntando i 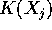 si trova quindi
che
si trova quindi
che
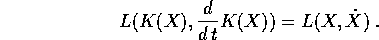
Consideriamo un sottogruppo ad un parametro di traslazioni,
per esempio nella direzione dell'asse coordinato numero h,
con h=1,2,3:
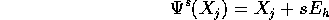
la cui derivata rispetto a s è il versore 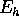 , per cui
la formula del teorema di Noether fornisce l'integrale:
, per cui
la formula del teorema di Noether fornisce l'integrale:

che è la coordinata lungo l'asse 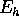 del vettore P
della quantità di moto
del vettore P
della quantità di moto

Da 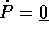 si deduce che il
centro di massa
si deduce che il
centro di massa 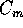
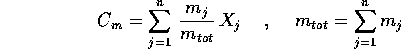
si muove di moto rettilineo uniforme.
Le coordinate del centro di massa sono integrali primi,
anche se dipendenti dal tempo:
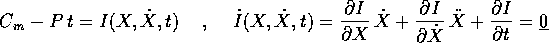
e quindi l'esistenza dei tre integrali primi della quantità
di moto consente di eliminare sei variabili, cioè di ridursi
ad un sistema dinamico in 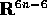 .
.
Se invece consideriamo un sottogruppo ad un parametro di
rotazioni attorno ad uno stesso asse 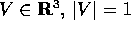 :
:

dove 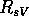 indica una rotazione di s radianti attorno
all'asse V (in verso antiorario visto dalla testa di V),
allora la derivata rispetto ad s, calcolata per s=0, è
espressa dalla
regola della velocità angolare , cioè dal
prodotto vettore
indica una rotazione di s radianti attorno
all'asse V (in verso antiorario visto dalla testa di V),
allora la derivata rispetto ad s, calcolata per s=0, è
espressa dalla
regola della velocità angolare , cioè dal
prodotto vettore
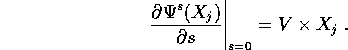
La formula del teorema di Noether fornisce l'integrale
primo:
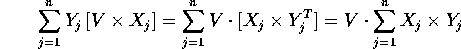
ossia la coordinata lungo l'asse V del vettore
momento angolare
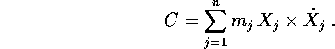
Usare i tre integrali primi corrispondenti alle tre
coordinate del vettore momento angolare per ridurre la dimensione
dello spazio delle fasi è assai meno facile che nel caso
della quantità di moto; il problema sarà discusso nella
Sezione 7.1.




Next: 6.5 SISTEMI HAMILTONIANI
Up: 6 SISTEMI CONSERVATIVI: PIÙ
Previous: 6.3 VINCOLI E COORDINATE
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
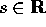


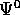 è l'identità su W, e che
è l'identità su W, e che
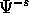 è l'inverso di
è l'inverso di 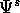 .
.
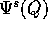 deve avere continue non solo le derivate rispetto
a t e alle coordinate di Q, ma anche quelle miste
deve avere continue non solo le derivate rispetto
a t e alle coordinate di Q, ma anche quelle miste
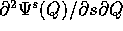 .
.
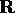 ed il gruppo
dei diffeomorfismi è un omomorfismo di gruppi.
ed il gruppo
dei diffeomorfismi è un omomorfismo di gruppi.
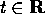 è un gruppo
ad un parametro di diffeomorfismi.
è un gruppo
ad un parametro di diffeomorfismi.
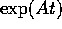 di un sistema
dinamico lineare
di un sistema
dinamico lineare 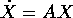 è un gruppo ad un parametro di
trasformazioni lineari; infatti il determinante
dell'esponenziale di matrice è sempre
diverso da zero per la
è un gruppo ad un parametro di
trasformazioni lineari; infatti il determinante
dell'esponenziale di matrice è sempre
diverso da zero per la 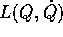 , definita su di uno spazio delle
fasi della forma
, definita su di uno spazio delle
fasi della forma 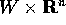 (W aperto di
(W aperto di 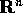 ), un
gruppo ad un parametro di simmetrie
è un gruppo ad un parametro
), un
gruppo ad un parametro di simmetrie
è un gruppo ad un parametro 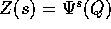 , la velocità si trasforma in modo
covariante :
, la velocità si trasforma in modo
covariante :

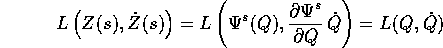
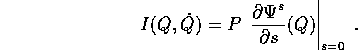
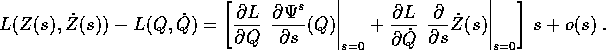
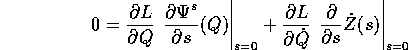
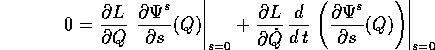
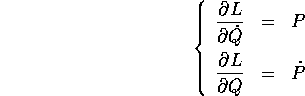
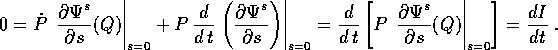
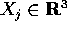 e masse
e masse 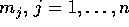 ; indicheremo con X il vettore di
; indicheremo con X il vettore di 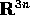 formato
giuntando gli
formato
giuntando gli 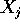 . L'energia cinetica è
. L'energia cinetica è
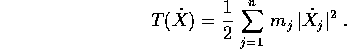
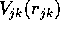 , dove
, dove
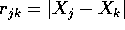 è la distanza dei due. Inoltre supponiamo
che valga la legge di azione e reazione
è la distanza dei due. Inoltre supponiamo
che valga la legge di azione e reazione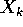 è uguale e contraria
a quella esercitata da
è uguale e contraria
a quella esercitata da 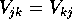 .
.
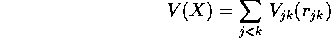
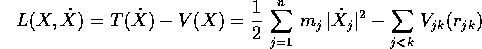
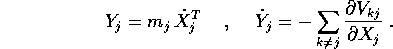
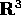 che sia un'
che sia un'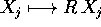 e di una
traslazione
e di una
traslazione 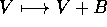 , cioè nella forma
, cioè nella forma
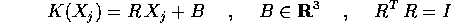
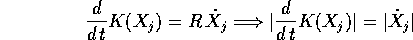
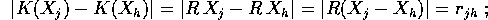
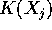 si trova quindi
che
si trova quindi
che
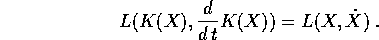
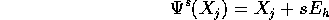
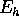 , per cui
la formula del teorema di Noether fornisce l'integrale:
, per cui
la formula del teorema di Noether fornisce l'integrale:


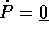 si deduce che il
centro di massa
si deduce che il
centro di massa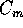
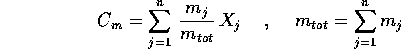
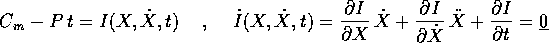
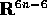 .
.
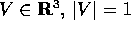 :
:

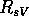 indica una rotazione di s radianti attorno
all'asse V (in verso antiorario visto dalla testa di V),
allora la derivata rispetto ad s, calcolata per s=0, è
espressa dalla
indica una rotazione di s radianti attorno
all'asse V (in verso antiorario visto dalla testa di V),
allora la derivata rispetto ad s, calcolata per s=0, è
espressa dalla