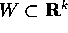Sommario I sistemi newtoniani sono ottenuti come modello di un sistema di punti soggetti ad una forza totale che ne influenza linearmente le accelerazioni. La matrice associata a questa relazione lineare contiene tutte le informazioni sulle masse dei corpi. Se la forza è conservativa, cioè deriva da un potenziale, le stesse equazioni possono essere espresse come equazioni di Lagrange, definendo la funzione lagrangiana come differenza fra l'energia cinetica e l'energia potenziale. I vantaggi del formalismo lagrangiano si apprezzano, per esempio, nella facilità di cambiare le coordinate che descrivono lo stato del sistema.
Consideriamo un sistema il cui stato sia univocamente descritto da un
vettore X con k coordinate: si dice che in tal caso il sistema ha
k gradi di libertà e l'insieme degli
stati possibili, che supporremo un aperto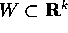 
, si dice
spazio delle configurazioni .
Studieremo dei sistemi dinamici che derivano da equazioni
differenziali del secondo ordine su W: la condizione iniziale è un
vettore a 2k componenti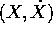 
nello spazio delle fasi , che
è un aperto di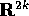 
e che supporremo del tipo 
.
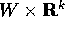La seconda equazione di Newton,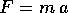 
, può essere adottata per
modellare l'evoluzione di un corpo puntiforme: se F è la somma
vettoriale delle forze che agiscono sul corpo, si postula che il punto
evolva lungo una curva per la quale il vettore accelerazione sia
sempre proporzionale al vettore F. Un simile modello non può
essere utilizzato in un qualunque sistema di riferimento, poiché dal
sistema di coordinate dipende la misura delle posizioni, le velocità
e le accelerazioni. In particolare, il modello valido in un sistema
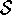non lo è generalmente in un sistema 
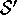variabile
nel tempo (per esempio, accelerato rispetto a 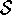). L'equazione
di Newton definisce perciò anche la classe dei sistemi di
riferimento (sistemi inerziali ) nei quali il modello è
applicabile. Un corpo complesso può essere modellato, per esempio,
come insieme di corpi puntiformi, ai quali - in un sistema inerziale -
si applica la legge di Newton.
Il formalismo della meccanica si basa sull'unica ipotesi che esista un sistema di coordinate inerziale, in cui si applicano le equazioni di Newton, e cerca di trasformare le equazioni differenziali in altre forme più maneggevoli, dal punto di vista del calcolo delle soluzioni e dello studio delle loro proprietà qualitative.
In genere, chiamiamo sistema newtoniano il sistema di equazioni
differenziali definito da un campo vettoriale di forze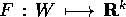 
, che definisce il sistema di equazioni
differenziali ordinarie del secondo ordine
dove M è una matrice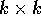 
che esprime la
relazione lineare tra accelerazione e forza; per questo M sarà
chiamata massa . Per esempio,
nel caso di un punto materiale di massa m che si muove nello
spazio ordinario, è k=3 ed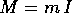 
(con I matrice
identità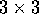 
).
Nel caso di un sistema di n corpi puntiformi con masse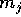 
si ha
k=3n: il vettore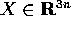 
è ottenuto accostando i vettori
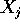di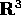 
della posizione di ciascun corpo, e la matrice M ha
dei blocchi 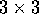lungo la diagonale principale della forma
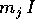, ovvero
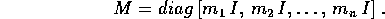
In genere M potrebbe anche non essere diagonale; le sole proprietà che useremo per sviluppare il formalismo sono che M è simmetrica e definita positiva.
Un caso molto importante è quello in cui la forza F(X)
è un campo vettoriale conservativo , ossia
ammette un potenziale: allora esiste una funzione V(X) (di classe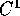 
) che
esprime l'energia potenziale del sistema, tale che
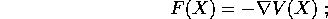
si noti il segno meno. In questo caso si parla di sistema newtoniano conservativo , e le equazioni di Newton sono
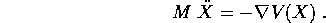
Al contrario di quanto accade con un solo grado di libertà, cioè per k=1, la condizione di ammettere potenziale non è banale. Il campo F(X) deve soddisfare in ogni punto una condizione espressa da un'equazione alle derivate parziali: precisamente, deve annullarsi il rotore
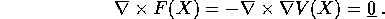
Il termine ``conservativo'' viene usato qui in un senso apparentemente diverso da quello che ha nel contesto dei sistemi dinamici conservativi , ma in effetti un sistema newtoniano con campo di forze conservative è dinamicamente equivalente ad un sistema dinamico conservativo, come sarà dimostrato nella Sezione 8.6.
Dalla presenza di un'energia potenziale si deduce l'esistenza di un integrale primo , l'integrale dell'energia : basta sommare all'energia potenziale l'energia cinetica
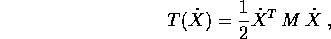
ovvero la
forma quadratica nelle velocità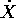 
la cui matrice
è M/2,
per ottenere l'energia (o energia totale )
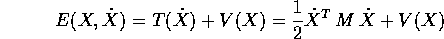
che ha derivata totale nulla:
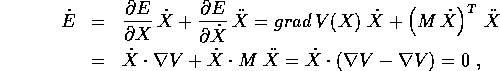
poich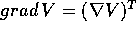é 
e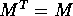 
.
Questo calcolo riuscirebbe più chiaro se si
decidesse una volta per tutte se si vogliono utilizzare i
gradienti come vettori riga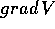 
o come vettori
colonna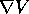 
. Per decidere questo, bisogna anche
decidere se le equazioni di moto sono un vettore riga o
colonna. Nell'ambito del formalismo newtoniano non c'è
una buona ragione per preferire l'una o l'altra
convenzione; come vedremo, nell'ambito del formalismo
lagrangiano la scelta è chiara.
La dinamica di un
sistema lagrangiano
è definita da una funzione
lagrangiana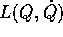 
, definita per 
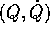in un
aperto di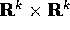 
:
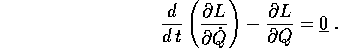
Queste equazioni di Lagrange sono un modo sintetico di scrivere k equazioni differenziali ordinarie del secondo ordine, che gode della vantaggiosa proprietà di avere una forma invariante per una vasta classe di cambiamenti di coordinate (cioè di sistema di riferimento) nello spazio delle configurazioni . Più in generale, vale il
Teorema di covarianza delle equazioni di Lagrange :
Sia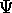 
un'applicazione differenziabile di classe 
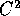tra
l'aperto W di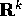 
e l'aperto Z di 
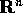, con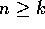 
:
Allora se valgono le equazioni di Lagrange nelle variabili X, valgono anche quelle nelle variabili Q:
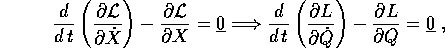
dove le due funzioni 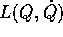e 
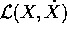si
corrispondono per valore :
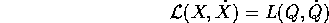
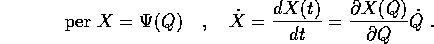
In questo enunciato non è richiesto che sia n=k. Nel caso di un cambiamento di coordinate, cioè per k=n e matrice jacobiana invertibile, il teorema si può applicare anche al cambiamento di coordinate inverso: allora le due equazioni di Lagrange sono equivalenti ed esprimono la stessa dinamiche equivalenti .
Dimostrazione:
La relazione tra la velocità 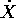e la
velocità generalizzata 
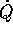è
ossia il vettore velocità si trasforma in modo controvariante . Le matrici delle derivate parziali sono:
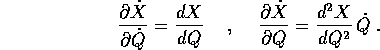
Le componenti delle derivate parziali seconde delle X rispetto alle
Q formano una tabella a tre indici, che moltiplicata per
il vettore 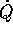restituisce una matrice: questa è la
maggiore complicazione che si introduce passando dal caso
k=1, svolto nella Sezione 5.3, al
caso k>1, anche se la dimostrazione è
formalmente identica.
I momenti coniugati alle variabili Q si ottengono da
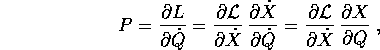
con derivata totale
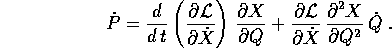
Per completare le equazioni di Lagrange nelle Q occorre calcolare l'altra parte del gradiente di L:
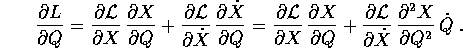
Togliendo da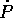 
si ottiene
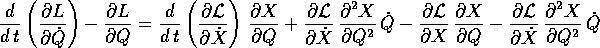
Ora bisogna utilizzare il fatto che i termini contenenti le derivate seconde della trasformazione si cancellano; si noti che questo accade perché le derivate miste in croce sono uguali, anche se questo è stato un po' nascosto dalla notazione sintetica che abbiamo adottato. Allora i termini che restano danno:
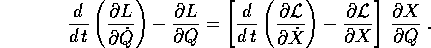
Perciò se valgono le equazioni di Lagrange per le X, cioè si annulla il primo fattore nella formula qui sopra, dopo la moltiplicazione per la matrice jacobiana si avrà ancora un vettore nullo, quindi le equazioni di Lagrange varranno anche per le Q.
Il primo membro delle equazioni di Lagrange è covariante : in altri termini, si trasforma come un gradiente (o una forma differenziale lineare) rispetto ad un cambiamento di coordinate, dovendo essere moltiplicato a destra per la sua matrice jacobiana. Questa è la ragione per cui conviene considerarlo come un vettore riga, in modo che la legge di trasformazione possa essere espressa come una moltiplicazione righe per colonne con la matrice jacobiana.
Le equazioni di Newton con campo di forze conservativo possono essere scritte in forma lagrangiana, rispetto alle opportune coordinate: la lagrangiana è la differenza fra l'energia cinetica e l'energia potenziale
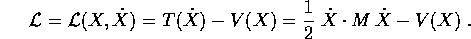
Allora il gradiente di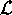 
rispetto alla velocità
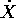(cioè la quantità di moto) è il vettore riga
e le equazioni di Lagrange diventano
dove il vettore zero va inteso come vettore riga. Pur di intenderle come vettore riga anziché come vettore colonna, sono quindi la stessa cosa delle equazioni di Newton.
Possiamo infine applicare il teorema di covarianza per descrivere tutte le lagrangiane che derivano dall'applicazione di un cambiamento di coordinate ad un sistema newtoniano. Se nelle variabili X la lagrangiana è della forma
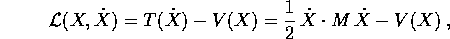
allora sostituendo alle velocità 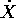la loro espressione
in funzione di nuove variabili 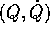, con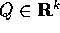 
:
nell'energia cinetica, si trova:
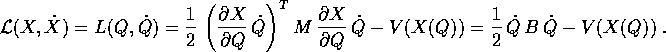
La nuova matrice B della forma quadratica nelle
che rappresenta l'energia cinetica è
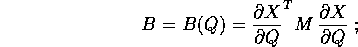
B è una matrice 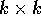, simmetrica e definita positiva (poiché
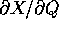ha rango k), ma con coefficienti che
dipendono da Q.
Perciò, in genere, lo studio di di sistemi lagrangiani che derivano da sistemi newtoniani richiede di considerare lagrangiane della forma
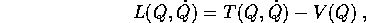
dove T è una forma quadratica omogenea e definita positiva nelle
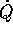; di una lagrangiana di questa forma si dice che
proviene da un sistema newtoniano .
Se ancora più generalmente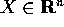 
, con n>k, (per
esempio se si cambiano solamente alcune coordinate e ci si restringe
ad esse) il ragionamento che precede è ugualmente valido, a
condizione che la persistenza della relazione X=X(Q) sia garantita
da dei vincoli .