We now proceed to compute the differential, at the nominal orbit, of
the map onto the MTP, with the formulas of Section 2, and we compute
the confidence ellipse
![]() ,
for
,
for ![]() .
The ellipse
has very uneven semiaxes, the short one being only
.
The ellipse
has very uneven semiaxes, the short one being only
![]() km,
while the long one is
km,
while the long one is
![]() km long; this is not
unexpected, since the conditioning number of the covariance matrix of
the orbital elements grows at least quadratically with time (see Paper
I, Section 4.1); intuitively, the orbital error accumulates along
track as an effect of the original uncertainty in the semimajor axis.
The good news is, the direction of the major axis of the confidence
ellipse is not directed towards the origin in the MTP, where the Earth
is; it is directed away from it by an angle
km long; this is not
unexpected, since the conditioning number of the covariance matrix of
the orbital elements grows at least quadratically with time (see Paper
I, Section 4.1); intuitively, the orbital error accumulates along
track as an effect of the original uncertainty in the semimajor axis.
The good news is, the direction of the major axis of the confidence
ellipse is not directed towards the origin in the MTP, where the Earth
is; it is directed away from it by an angle
![]() .
Since
the ellipse is very narrow, almost a segment, the minimum distance
from the linear analysis is essentially the nominal minimum distance
dn times
.
Since
the ellipse is very narrow, almost a segment, the minimum distance
from the linear analysis is essentially the nominal minimum distance
dn times
![]() ,
in this case
,
in this case ![]() AU. If the linear
approximation is applicable, then
AU. If the linear
approximation is applicable, then
![]() is all what
matters, while both dn and
is all what
matters, while both dn and ![]() can change for solutions
using different data sets. If
can change for solutions
using different data sets. If
![]() is safely above the
surface of the Earth, this is enough to conclude that the risk of
impact is essentially zero
1.
is safely above the
surface of the Earth, this is enough to conclude that the risk of
impact is essentially zero
1.
 |
To see whether this conclusion holds, even when taking into account the
nonlinearity of the map onto the MTP, we have computed the semilinear
confidence boundary
![]() ,
for the same
,
for the same
![]() .
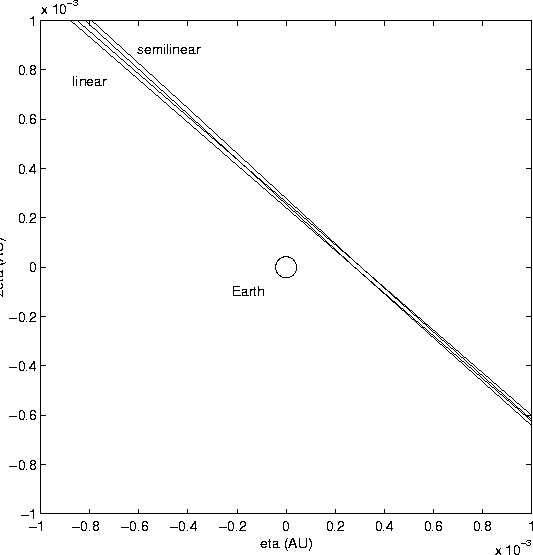
Figure 3 shows a square window on the MTP
with a side of about
.
Figure 3 shows a square window on the MTP
with a side of about ![]() km; the Earth is the circle around the
center, drawn at the same scale. The linear and semilinear confidence
boundaries are almost the same near the nominal solution (which is
along the
km; the Earth is the circle around the
center, drawn at the same scale. The linear and semilinear confidence
boundaries are almost the same near the nominal solution (which is
along the ![]() axis, towards the right in the Figure); the
semilinear boundary begins to bend with respect to the major axis of
the ellipse, until at a distance of about
axis, towards the right in the Figure); the
semilinear boundary begins to bend with respect to the major axis of
the ellipse, until at a distance of about ![]() km the two
confidence regions do not overlap at all. Near the Earth, however, the
two boundaries are essentially the same: this implies that the
conclusion on the essentially zero risk of impact is valid, in this
case, also within a nonlinear model.
km the two
confidence regions do not overlap at all. Near the Earth, however, the
two boundaries are essentially the same: this implies that the
conclusion on the essentially zero risk of impact is valid, in this
case, also within a nonlinear model.
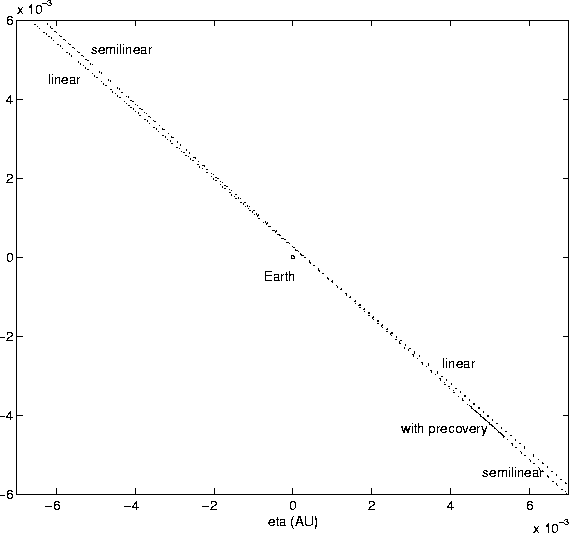 |
To decide whether the applicability of the linear approximation is a
general result, rather than an accidental property of this example, we
have plotted the entire confidence boundaries
Klin(3) and
KN(3) in Figure 4; to this purpose, we have used a
window on the MTP with a side of about
![]() km. This makes
clear that the distance of the 2028 closest approach, as assessed by
using only the 1997-98 data (until March 4, 1998), could well be up to
4 times the Earth-Moon distance. The plot also shows that the linear
ellipse and the semilinear confidence boundary can be far apart, near
the two extremities, by more than the diameter of the Earth. In other
words, the fact that the linear and the semilinear method give the
same answer to the question about the possibility of an impact depends
upon where the Earth is, with respect to the nominal solution and with
respect to the tips of the confidence ellipse.
km. This makes
clear that the distance of the 2028 closest approach, as assessed by
using only the 1997-98 data (until March 4, 1998), could well be up to
4 times the Earth-Moon distance. The plot also shows that the linear
ellipse and the semilinear confidence boundary can be far apart, near
the two extremities, by more than the diameter of the Earth. In other
words, the fact that the linear and the semilinear method give the
same answer to the question about the possibility of an impact depends
upon where the Earth is, with respect to the nominal solution and with
respect to the tips of the confidence ellipse.
Thus Figure 4 allows us to conclude: (1) that the impact risk by 1997 XF11 in 2028 is essentially zero, even using the 1997-98 observations only; (2) that the close approach of October 2028 is not constrained, by the 1997-98 observations, to be at a distance closer than the Moon; (3) that the linear approximation, successful as it is in this case, can not be relied upon in every case. All three conclusions have been also obtained by the Monte Carlo method [Muinonen and Bowell 1993]2.