3 Non-resonant returns

Because of the low nodal distance also at the descending node, there is the possibility of a non-resonant return. This can occur if the Earth completes h+1/2 revolutions while the asteroid completes k+1/2 revolutions, so that they are both at the descending node at the same time. Taking into account the eccentricities of both orbits, the time required to go from the ascending node to the descending node is for the Earth (not exactly half a year), and for the asteroid (much more than half a period). Again allowing for the timing of the 2027 encounter, the condition to be satisfied for an encounter at the descending node is .

If we add the condition that the distance is zero at both nodes, we have 4 conditions on the 5 variables , where are the eccentric anomalies at the nodes, and we can explicitly compute as a function of a. Thus the above condition defines a curve in the plane, as in the resonant case. Figure 4 shows all the possible non-resonant returns after the 2027 encounter with , that is taking place until February 2040. By explicitly listing the non-resonant returns (with the global method described below) we find that the approximations used in this computation result in errors too small to be clearly visible at the scale of the figure.

 
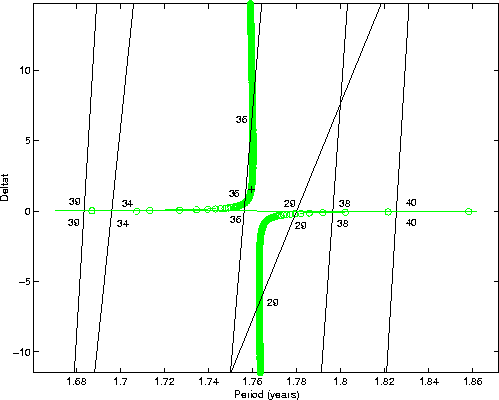
Figure 4:  Non-resonant returns of 1999 AN at the descending node after the 2027 encounter, taking place until February 2040. The circles and the solid line represent the alternate solutions along the variations line as in the previous Figure. The non-resonant returns are the intersections labelled with the year (after 2000) in which the return takes place.

Combining the 11 resonant returns of Figure 3 and the 14 non-resonant ones of Figure 4, our theory predicts a total of 25 close approach solutions. For each one of these we could perform a close approach analysis like the one of Figures 2. However, for the purpose of determining the closest approach distance, this is not necessary, because the minimum distance is essentially the local MOID near the relevant node; it is also not sufficient to identify all the possible returns, because of course a secondary return from a previous return is possible, and so on. For this reason we have devised a global method to search for all the returns at once.

We started from the same catalog of alternate orbital solutions, evenly distributed in the interval , used in the Figures 3 and 4. Each solution was propagated forward from the 2027 encounter, recording the position and the nodal distances every time the Earth is passing at the nodes. We determine if there was a crossing of the relevant node (near that time) by the changes of sign of the z coordinate in an ecliptic reference frame, as in Figure 1. We interpolate between these adjacent solutions to find the value corresponding to the node crossing at the time when the Earth is there. We similarly obtain the minimum distance between the orbit of the Earth and of the asteroid around the relevant node. By a continuity argument, if z changes sign between two solutions at and , there is an intermediate value of for which z is zero, that is at least one solution along the variations line always exists that passes at a distance from the Earth as low as the local MOID (even slightly less, due to gravitational focusing).

This argument cannot be applied for values of |z| too large, otherwise the two consecutive solutions could be out of phase by more than one period. Thus the limit of the method is the stretching, which is the ratio between the distance in physical space of two points on two orbits (at the same time) and the distance of the corresponding values of , which parametrises the variations line. For , as in our solutions catalog, a stretching in physical space of AU would result in two consecutive orbits being out of phase by 1 revolution. After a very close approach such values of the stretching do occur, and even more after a sequence of close approaches. For this reason we have densified our sampling of the variations line in the region of high stretching around the solution with the closest approach in 2027, namely for , by computing another alternate orbits. With , even returns with stretching coefficients more than AU can be detected.

Table I presents all the returns up to August 2040 that we have found with this method, using both the catalog and the denser catalog. The stretching listed in the Table is not the one computed with distances in the 3-dimensional space, but its projection upon the MTP, which is in a fixed ratio to the spatial stretching. That is, we use the product of the time difference in the node crossing and the relative encounter velocity (0.0149 AU/day) divided by . This MTP stretching allows to compute in units the size of the interval along the variation line where approaches within a given distance occur. Given a probability density function, this results in a probability of such an event; in the Table we have used the uniform distribution described above to estimate the probability of an encounter within the mean distance of the Moon. Note that the lower the stretching, the higher the probability of an encounter within a given distance, thus shallow encounters can be more effective in generating likely returns than the deep ones.

Each of the 25 returns predicted by our theory appear in the Table, with MTP stretching . 6 solutions not predicted by Figures 3 and 4 appear; they can all be interpreted as secondary returns, e.g. the third solution for February 2036 is a non-resonant return after the 2034 encounter. Both 5/3 and 2/1 returns become possible after the 2034 encounter.

Among these secondary returns there is one in August 2039 for which the interpolated MOID is less than the radius of the Earth. Since the stretching is extreme, we have checked by performing close approach analysis as in Figure 2, and verified that a collision solution actually exists. The high stretching, however, appears as divisor in the formula for the probability, and this results in an estimate of the probability for this impact of the order of . The possibility of such an impact could be frightening, but if we assume that the probability of an impact by an undiscovered 1 km asteroid is of the order of per year [11], the probability of an impact by 1999 AN in 2039 is less than the probability of being hit by an unknown asteroid within the next few hours.

The stretching coefficients used in this paper are closely related to the adimensional stretching used in the computations of the Lyapounov characteristic exponents: they differ only by a constant factor, that is the stretching at some initial epoch. Thus the data in the Table indicate the level of chaos of each return orbit. Each of the close approaches listed in the Table can in turn be analysed for its own resonant and nonresonant returns, and so on. This is precisely the process leading to a fractal structure of encounters in the -space. It is clear that the cascade of successive returns could be described by a symbolic dynamics, as in other chaotic celestial mechanics problems [12].