Sommario Le equazioni tipiche della meccanica - e di molti altri modelli matematici di problemi fisici - non si presentano nella forma di equazioni di Hamilton, ma sono espresse direttamente in termini di derivate prime e seconde delle coordinate. Tuttavia, se le equazioni possono essere ricavate dalla definizione di una energia cinetica ed una energia potenziale, esse possono sempre essere espresse nella forma detta di Lagrange. Le equazioni di Lagrange possono a loro volta, sotto certe condizioni, essere equivalenti ad equazioni di Hamilton.
La seconda delle equazioni di Hamilton fornisce una relazione
tra il momento p della coordinata q, e la sua
velocità generalizzata ,
cioè la derivata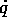 
:
Supponiamo che la funzione H(p,q) sia di classe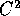 
e
strettamente convessa, se considerata come funzione della
sola p, per q fisso. Allora la trasformazione che
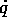esprime la in funzione della p è monotona
crescente:
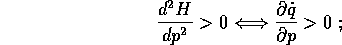
e va sotto il nome di trasformazione di Legendre :
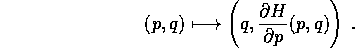
Questo è esattamente quello che abbiamo fatto nel caso
newtoniano: se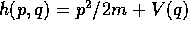 
, allora la seconda equazione di
Hamilton dice che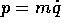 
e quindi tra i due piani 
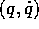e
(p,q) c'è una trasformazione che consiste semplicemente in un
cambiamento di scala, accompagnato dallo scambio dell'ordine degli
assi. La condizione di convessità consente di generalizzare questa
trasformazione anche nel caso in cui la relazione tra 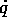e p
sia nonlineare.
Ne segue che la dinamica del sistema dinamico hamiltoniano può
essere descritta anche nelle coordinate 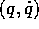anziché
(p,q). Il problema è come trasformare le equazioni di Hamilton nel
piano (p,q) in equazioni che descrivano la stessa dinamica nel piano
.
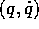Il sistema dinamico nel piano 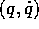si può scrivere in modo
molto efficiente come equazione del secondo ordine:
occorre definire la lagrangiana
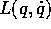che può essere descritta geometricamente
come l'opposto dell'ordinata all'origine della retta tangente al grafico
dell'hamiltoniana (si intende sempre per un valore fissato di q),
come indicato in Figura 5.4. Quindi la relazione tra
H(p,q) ed L(q,u) (indicando con u la variabile che svolge il ruolo
di 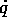) è data dall'equazione della tangente alla curva h=H(p)
(con q fisso) che è:
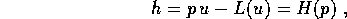
ossia, indicando anche la dipendenza da q e riscrivendo 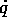al
posto di u:
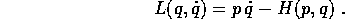
Si noti che se vale la condizione di convessità, per cui la
relazione tra p e 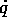è invertibile, la formula qua sopra
può essere usata nei due sensi. Può essere la definizione di
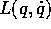se si conosce in modo esplicito H(p,q); in tal caso occorre
sostituire a p la sua espressione in termini di 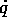. Ma se al
contrario si conosce 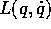, la stessa formula definisce H(p,q), pur
di sostituire a 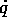la sua espressione in funzione di p. Questa
relazione involutiva tra le due funzioni H(p,q) ed 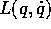si designa
con il nome di trasformata di Legendre .
Esempio:
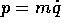, quindi 
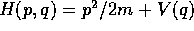corrisponde a
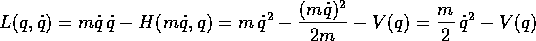
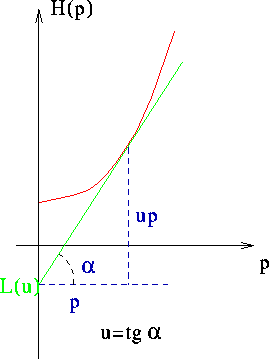
Figure 5.4: La trasformata di Legendre si può esprimere
geometricamente mediante l'intersezione della retta tangente al
grafico di una funzione con l'asse delle ordinate.
Dobbiamo ora ricavare l'equazione di Lagrange , che esprime
- in termini della funzione di Lagrange - la dinamica nel piano
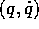. Calcoliamo le derivate parziali della funzione di
Lagrange, tenendo conto della dipendenza di p sia da q che da 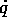per effetto della inversa della trasformazione di Legendre:
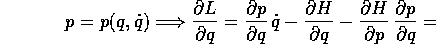
che si semplifica perché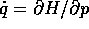 
in
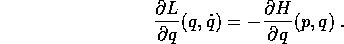
Si intende che la relazione qui sopra vale con i due membri calcolati nei punti corrispondenti - per la trasformazione di Legendre - nei due piani.
In modo analogo
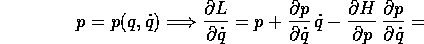
si semplifica usando la trasformazione di Legendre, e si riduce a:
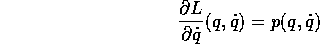
che esprime l'inversa della trasformazione di Legendre. Resta ora da utilizzare la prima delle equazioni di Hamilton:
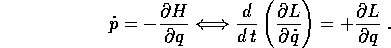
In conclusione le equazioni di Hamilton nel piano (p,q),
e l'equazione di Lagrange nel piano :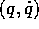
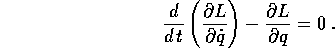
esprimono dinamiche equivalenti nei due sistemi di coordinate, nel senso che la trasformazione di coordinate (un diffeomorfismo ) manda le soluzioni dell'una nelle soluzioni dell'altra, lo stesso fa la trasformazione inversa. Si parla della dinamica di un sistema quando ci si riferisce alle soluzioni, senza aver bisogno di precisare il sistema di coordinate in cui sono espresse, cioè senza scegliere tra le possibili dinamiche equivalenti.
L'equazione di Lagrange è un'equazione differenziale del secondo
ordine; per ricavare il corrispondente sistema dinamico nel piano
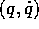occorre considerare che il momento p è funzione di ,
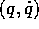quindi
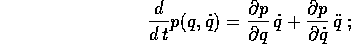
sostituendo nell'equazione di Lagrange
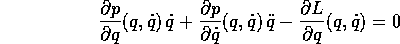
è della forma risolubile rispetto alla derivata seconda,
quando non si annulla il coefficiente di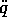 
, cioè se:
La condizione di non annullamento della derivata seconda della
funzione di Lagrange rispetto a 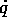è la condizione di
convessità che assicura che l'inversa della trasformazione di
Legendre è monotona crescente. Quindi tale condizione è
equivalente alla condizione di convessità su H come funzione di
p, cioè al non annullamento della derivata seconda della funzione
di Hamilton rispetto a p.
Esempio:
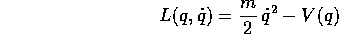
e quindi l'equazione di Lagrange è semplicemente
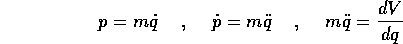
cioè l'equazione di Newton per un corpo di massa m soggetto ad un campo di forze con potenziale -V(q).
Esercizio Date le hamiltoniane scrivere la corrispondente lagrangiana e l'equazione di Lagrange.
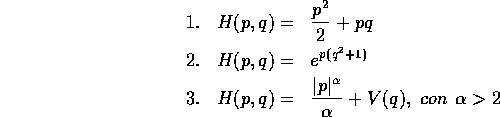
Esercizio Date le lagrangiane
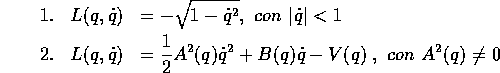
scrivere la corrispondente hamiltoniana e le equazioni di Hamilton. (Soluzione)
La coordinata q parametrizza lo spazio delle configurazioni, ma
naturalmente la scelta di un altra coordinata è possibile.
Supponiamo che x=x(q) sia un cambiamento di coordinata, espresso da
una funzione differenziabile, invertibile e con inversa differenziabile;
questo implica che la derivata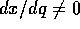 
. Supponiamo che la
funzione di Lagrange 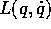si trasformi in 
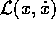, nel
senso che le due funzioni hanno lo stesso valore nei punti
corrispondenti:
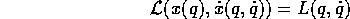
Teorema di covarianza dell'equazione di Lagrange :
Sia x=x(q) un cambiamento di coordinata (con 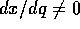) di
classe 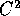; sia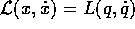 
. Allora l'equazione di
Lagrange nelle variabili q, e l'equazione di Lagrange nella variabile x,
esprimono dinamiche equivalenti :
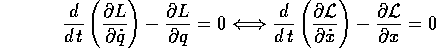
Dimostrazione:
con derivate parziali:
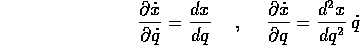
È nel calcolo di queste derivate parziali che si sfrutta
l'ipotesi che il cambiamento di coordinate sia .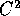
Per trovare la formula di trasformazione dell'equazione di Lagrange basta usare le derivate di funzioni composte: per il momento p coniugato alla coordinata q
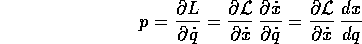
la cui derivata totale è
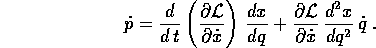
Per completare l'espressione dell'equazione di Lagrange nella q in
termini della funzione trasform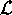ata 
occorre calcolare anche
l'altra derivata:
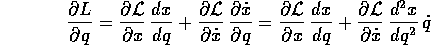
e poi mettere insieme l'equazione di Lagrange per la variabile q:
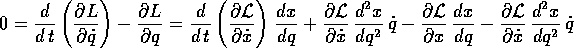
in cui i due termini con la derivata seconda del cambiamento di coordinata si cancellano, e resta
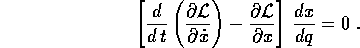
da cui la tesi, poiché 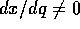.