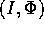 :
:
Sommario Aggiungendo ad un sistema hamiltoniano integrabile una perturbazione, dipendente da un piccolo parametro, si ottengono soluzioni che possono essere calcolate (in modo approssimato al primo ordine nel piccolo parametro) con un'equazione integrabile per quadratura. La quadratura può essere eseguita termine a termine se la funzione perturbatrice è espressa mediante una serie di Fourier; tuttavia non è facile dimostrare la convergenza della serie che esprime la soluzione, poiché essa dipende dalla presenza di un reticolo denso di risonanze.
Dato un sistema hamiltoniano integrabile , possiamo supporre
che sia scritto direttamente nelle variabili azione-angolo
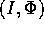 :
:
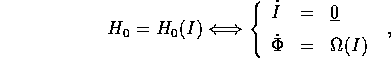
dove 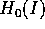 è una qualunque funzione di classe
è una qualunque funzione di classe 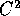 su un aperto
D di
su un aperto
D di 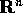 . Supponiamo ora di aggiungere al sistema dinamico
una perturbazione che ne conservi il carattere hamiltoniano:
perturbiamo cioè la funzione di Hamilton come
. Supponiamo ora di aggiungere al sistema dinamico
una perturbazione che ne conservi il carattere hamiltoniano:
perturbiamo cioè la funzione di Hamilton come
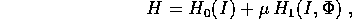
dove la parola ``perturbazione'' significa semplicemente che siamo
interessati al caso in cui il parametro reale 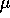 è ``piccolo'',
in un senso che sarà precisato tra breve. La funzione
è ``piccolo'',
in un senso che sarà precisato tra breve. La funzione 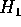 dipende
sia dalle azioni I che dalle
dipende
sia dalle azioni I che dalle 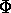 ; poiché queste ultime sono
variabili angolo ,
la funzione
; poiché queste ultime sono
variabili angolo ,
la funzione 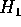 deve essere periodica di
periodo
deve essere periodica di
periodo 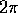 in ciascuna di esse. Oltre a ciò, supporremo che
in ciascuna di esse. Oltre a ciò, supporremo che
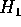 sia differenziabile (di classe
sia differenziabile (di classe 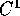 ) su un insieme della forma
) su un insieme della forma
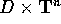 .
.
Le soluzioni del problema integrabile ``imperturbato''
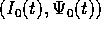 sono espresse, in funzione delle condizioni
iniziali
sono espresse, in funzione delle condizioni
iniziali 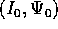 , da semplici scorrimenti
, da semplici scorrimenti
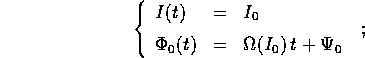
vogliamo calcolare una soluzione approssimata del problema perturbato
con hamiltoniana 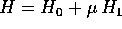 , che differisca dalla soluzione
esatta solo per termini dell'ordine di infinitesimo di
, che differisca dalla soluzione
esatta solo per termini dell'ordine di infinitesimo di 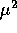 per
per
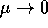 . Si noti che le soluzioni dipendono in modo differenziabile
dal parametro
. Si noti che le soluzioni dipendono in modo differenziabile
dal parametro 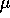 : basta aggiungere al sistema di equazioni
differenziali di Hamilton l'equazione
: basta aggiungere al sistema di equazioni
differenziali di Hamilton l'equazione 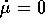 per trasformare
per trasformare
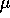 in una condizione iniziale, rispetto alla quale il flusso
integrale è differenziabile. Perciò possiamo espandere le soluzioni
in una condizione iniziale, rispetto alla quale il flusso
integrale è differenziabile. Perciò possiamo espandere le soluzioni
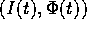 come
come
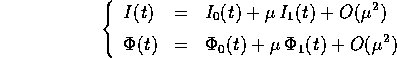
e cercare le equazioni differenziali a cui devono soddisfare le
``perturbazioni'' 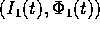 . Sostituendo nelle equazioni
di Hamilton con hamiltoniana
. Sostituendo nelle equazioni
di Hamilton con hamiltoniana 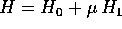 si ricava
si ricava
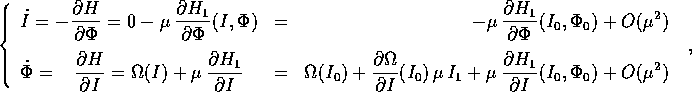
ed isolando la parte di ordine 1 in 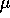 :
:
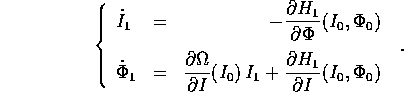
Queste equazioni perturbative sono equazioni differenziali
lineari dipendenti dal tempo (che appare nelle soluzioni imperturbate
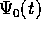 ); si noti che vi appaiono le derivate parziali delle
frequenze proprie
); si noti che vi appaiono le derivate parziali delle
frequenze proprie 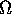 del sistema
imperturbato, cioè le derivate seconde di
del sistema
imperturbato, cioè le derivate seconde di 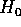 . Ma la proprietà
più importante è che le equazioni perturbative sono integrabili
per quadrature:
. Ma la proprietà
più importante è che le equazioni perturbative sono integrabili
per quadrature:
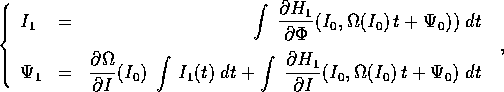
dove le espressioni integrande sono funzioni note di t.
Per precisione, nella seconda quadratura la funzione integranda
è nota solo dopo avere eseguito la prima quadratura ed aver ricavato
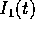 ; in altre parole, è sempre necessaria una
doppia quadratura .
; in altre parole, è sempre necessaria una
doppia quadratura .
In conclusione, anche se il sistema hamiltoniano 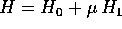 non
è integrabile, l'approssimazione del primo ordine
non
è integrabile, l'approssimazione del primo ordine 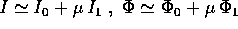 è calcolabile per
quadrature.
è calcolabile per
quadrature.
Una soluzione per quadrature dell'equazione perturbativa non è
sempre un metodo efficace per approssimare la soluzione, per
due motivi. In primo luogo, in generale non si può integrare una
funzione nota del tempo (ma con espressione molto complicata)
passando attraverso un'espressione analitica della primitiva, che non
è nota; né la quadratura numerica è necessariamente più
facile dell'integrazione numerica diretta delle equazioni di Hamilton.
Inoltre, la soluzione perturbativa è utile solo se risulta essere
``piccola'', ossia se i prodotti 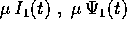 sono
effettivamente dell'ordine di
sono
effettivamente dell'ordine di 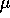 , il che non può essere garantito
per t grande; se questo non è vero, non c'è ragione di sperare
che il termine
, il che non può essere garantito
per t grande; se questo non è vero, non c'è ragione di sperare
che il termine 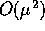 , che è stato trascurato, sia piccolo.
, che è stato trascurato, sia piccolo.
Entrambi i problemi possono essere affrontati utilizzando l'espansione
in serie di Fourier dell'equazione perturbativa. Abbiamo
già osservato che la funzione 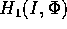 è periodica di periodo
è periodica di periodo
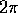 in ciascuno degli angoli
in ciascuno degli angoli 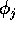 ; poiché tale funzione è
almeno
; poiché tale funzione è
almeno 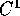 , per ogni I fissato esiste una serie di Fourier che
converge uniformemente su
, per ogni I fissato esiste una serie di Fourier che
converge uniformemente su 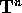 alla funzione perturbativa:
alla funzione perturbativa:
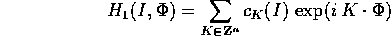
dove K è un multiindice , cioè un vettore con coefficienti
interi, ed i coefficienti di Fourier 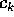 sono funzioni delle
variabili azione a valori complessi (invece delle esponenziali
complesse si potrebbero usare le funzioni trigonometriche reali
sono funzioni delle
variabili azione a valori complessi (invece delle esponenziali
complesse si potrebbero usare le funzioni trigonometriche reali
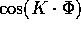 e
e 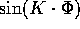 ). Si noti che il termine
costante rispetto a
). Si noti che il termine
costante rispetto a 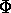 , cioè con
, cioè con 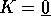 , si può
supporre nullo (altrimenti si aggiunge ad
, si può
supporre nullo (altrimenti si aggiunge ad 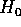 ).
).
Sostituendo nell'equazione perturbativa, si possono eseguire termine a
termine le derivate rispetto agli angoli 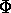 :
:
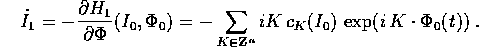
Quando si sostituisce 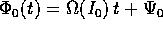 , la serie a
secondo membro diventa una serie di funzioni trigonometriche con
argomenti funzioni lineari di t. Se supponiamo di poter integrare
termine a termine, basta dividere ogni termine per la frequenza
, la serie a
secondo membro diventa una serie di funzioni trigonometriche con
argomenti funzioni lineari di t. Se supponiamo di poter integrare
termine a termine, basta dividere ogni termine per la frequenza
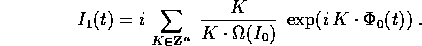
per ottenere un'espressione della perturbazione 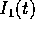 mediante una
serie: se questa serie è convergente, allora, per sostituzione nella
seconda equazione perturbativa, si ottiene un'altra quadratura
ugualmente eseguibile termine a termine, e si ricava un'espressione per
serie anche di
mediante una
serie: se questa serie è convergente, allora, per sostituzione nella
seconda equazione perturbativa, si ottiene un'altra quadratura
ugualmente eseguibile termine a termine, e si ricava un'espressione per
serie anche di 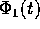 :
:
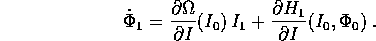
La difficoltà della quadratura viene sostituita dalla
difficoltà di calcolare i coefficienti di Fourier 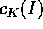 ; in molti
interessanti casi pratici ciò è possibile, anche se laborioso.
; in molti
interessanti casi pratici ciò è possibile, anche se laborioso.
Questo procedimento è stato usato per circa 150 anni, ad esempio per risolvere problemi esprimibili come perturbazioni del problema dei due corpi , come il moto dei pianeti attorno al Sole tenendo conto delle attrazioni reciproche dei pianeti. Soltanto al termine di tale periodo i matematici hanno tentato di rispondere alle domande, lasciate aperte anche in questa breve presentazione, sulla convergenza delle serie e sulla legittimità delle quadrature per serie.
Il contributo dei termini della serie che esprime le perturbazioni,
per esempio 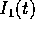 per le variabili azione,
dipende sia dal valore dei coefficienti di Fourier
per le variabili azione,
dipende sia dal valore dei coefficienti di Fourier 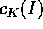 della
funzione perturbativa, sia dai moltiplicatori
della
funzione perturbativa, sia dai moltiplicatori

questi ultimi dipendono dalle frequenze del problema imperturbato, in particolare dal divisore
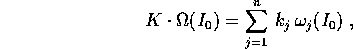
che è una combinazione diofantea (ossia con coefficienti
interi 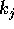 ) delle frequenze proprie
) delle frequenze proprie 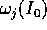 del sistema
integrabile che si ottiene per
del sistema
integrabile che si ottiene per 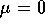 . Se si verifica una
risonanza , ossia se esiste un particolare multiindice K tale
che il divisore corrispondente si annulla, allora la perturbazione
. Se si verifica una
risonanza , ossia se esiste un particolare multiindice K tale
che il divisore corrispondente si annulla, allora la perturbazione
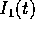 non è esprimibile come una serie trigonometrica. In effetti
se
non è esprimibile come una serie trigonometrica. In effetti
se 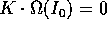 , il termine corrispondente di
, il termine corrispondente di 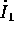 è
costante, e contribuisce all'integrale con una funzione lineare del
tempo: perciò
è
costante, e contribuisce all'integrale con una funzione lineare del
tempo: perciò 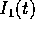 non è limitata (e
non è limitata (e 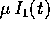 cessa
di essere piccola per t abbastanza grande), per cui l'espansione in
serie di potenze di
cessa
di essere piccola per t abbastanza grande), per cui l'espansione in
serie di potenze di 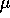 della soluzione non è
uniformemente convergente rispetto a t.
della soluzione non è
uniformemente convergente rispetto a t.
Questo risultato è abbastanza paradossale: per rendersene conto,
consideriamo il caso n=2 a due gradi di libertà, con le due sole
frequenze proprie 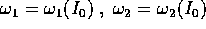 .
Fra tutti i divisori
.
Fra tutti i divisori

con 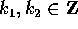 non entrambi nulli, si trova lo zero se e solo se
non entrambi nulli, si trova lo zero se e solo se
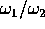 è razionale, ossia se il corrispondente
flusso di Kronecker ha tutte le orbite periodiche. Ma al
variare di
è razionale, ossia se il corrispondente
flusso di Kronecker ha tutte le orbite periodiche. Ma al
variare di 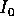 il rapporto
il rapporto 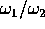 può variare, e
quindi passerà da valori razionali a valori irrazionali in modo
discontinuo, visto che sia
può variare, e
quindi passerà da valori razionali a valori irrazionali in modo
discontinuo, visto che sia 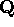 che
che 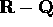 sono densi in
sono densi in 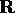 .
Dobbiamo concludere che il problema non è risolubile su nessun aperto
dello spazio delle condizioni iniziali?
.
Dobbiamo concludere che il problema non è risolubile su nessun aperto
dello spazio delle condizioni iniziali?
La risposta a questa domanda richiederebbe la conoscenza di alcuni dei risultati più profondi della matematica degli ultimi decenni; per vedere alcuni enunciati recenti, si può consultare l'appendice 8 di [Arnold 86].
Non appena compiuta, nel XIX secolo, la sistemazione rigorosa
del calcolo infinitesimale, ci si pose il problema di esprimere le
soluzioni di un sistema hamiltoniano qualsiasi mediante una serie di
funzioni del tempo t che fosse uniformemente convergente
per 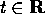 . Benché questa rappresentazione potrebbe avere molte
forme, l'idea era quella di dimostrare la convergenza della
rappresentazione per serie di una soluzione perturbativa, cioè
sviluppata in serie rispetto ad un piccolo parametro
. Benché questa rappresentazione potrebbe avere molte
forme, l'idea era quella di dimostrare la convergenza della
rappresentazione per serie di una soluzione perturbativa, cioè
sviluppata in serie rispetto ad un piccolo parametro 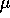 , in modo
che a
, in modo
che a 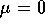 corrispondesse un sistema integrabile.
corrispondesse un sistema integrabile.
Definizione:
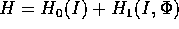 , con
, con 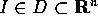 e
e 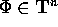 , si dice integrabile secondo Weierstrass
se ogni soluzione si può esprimere
, si dice integrabile secondo Weierstrass
se ogni soluzione si può esprimere
come serie di Taylor nel parametro 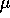
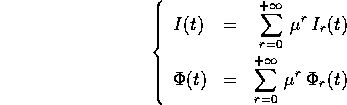
uniformemente convergente per 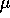 abbastanza piccolo.
Nella serie,
abbastanza piccolo.
Nella serie, 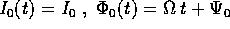 la soluzione per
la soluzione per
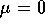 , e ciascuno dei termini di ordine r>0 `e esprimibile
mediante serie di funzioni trigonometriche uniformemente convergenti:
, e ciascuno dei termini di ordine r>0 `e esprimibile
mediante serie di funzioni trigonometriche uniformemente convergenti:
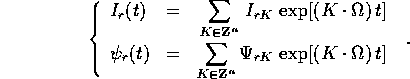
Si intende che le n frequenze proprie
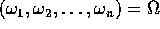 sono funzione delle
condizioni iniziali, ma costanti lungo ogni orbita.
sono funzione delle
condizioni iniziali, ma costanti lungo ogni orbita.
Il sistema si dirà invece non integrabile se una tale rappresentazione delle soluzioni non è possibile.
Conoscendo gli sviluppi in serie di Fourier usati nell'equazione perturbativa, sembra più facile mostrare che questi sono convergenti (sotto ipotesi opportune) piuttosto che dimostrare la non integrabilità; per ottenere una dimostrazione di quest'ultima occorre non solo dimostrare che un dato sviluppo in serie è divergente, ma che non è possibile trovarne un altro convergente.
Il re di Svezia, dietro suggerimento di Weierstrass e Mittag-Lefter, mise in palio un consistente premio per il primo matematico che fosse riuscito a dimostrare che il problema dei tre corpi puntiformi, che interagiscono solo con la mutua gravitazione, era integrabile (nel senso di Weierstrass). Nel 1889 il premio fu attribuito a H. Poincaré, che aveva dimostrato che il problema dei tre corpi era non integrabile.
Proprietà:
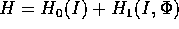 è integrabile nel senso del
teorema di Arnold-Jost , allora è integrabile anche nel
senso di Weierstrass.
è integrabile nel senso del
teorema di Arnold-Jost , allora è integrabile anche nel
senso di Weierstrass.
Problema
Dimostrare la proprietà precedente: la soluzione, espressa
mediante degli scorrimenti nelle variabili azione-angolo del teorema
di Arnold-Jost, si trasforma in una serie di Fourier (della forma
richiesta dalla definizione di Weierstrass) quando si passa alle
variabili 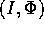 .
.
Anche l'implicazione inversa è vera, pur di aggiungere alcune ipotesi piuttosto tecniche sulla forma delle serie.