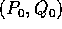7.5 PICCOLE OSCILLAZIONI

 

Sommario I sistemi dinamici lineari che si ottengono linearizzando dei sistemi conservativi hanno proprietà speciali, descrivibili in termini di esponenti di Lyapounov. Nel caso proveniente da un sistema newtoniano conservativo, le soluzioni possono essere descritte come sovrapposizione di oscillazioni armoniche.

Linearizzazione conservativa

Un punto di equilibrio 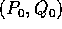 di un sistema hamiltoniano è un punto in cui si annulla il secondo membro, quindi corrisponde ad un punto stazionario della hamiltoniana:

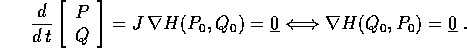
Il sistema linearizzato  nel punto di equilibrio

avrà per matrice 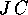, dove C è la matrice hessiana di H, calcolata nel punto di equilibrio, e J è la matrice che definisce la struttura simplettica . Le matrici della forma JC, con C simmetrica, hanno proprietà speciali per quanto concerne gli autovalori:

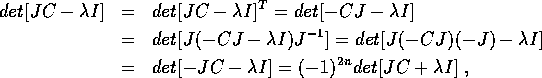
per cui se 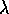è un autovalore di JC, anche 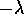è un autovalore, con la stessa molteplicità (e anche lo stesso numero di blocchi di Jordan della stessa dimensione). Quindi non tutti i sistemi dinamici lineari possono essere i linearizzati di sistemi hamiltoniani  ; per esempio pozzi e sorgenti non possono esserlo, perché per ogni esponente di Lyapounov  positivo deve essercene anche uno negativo, e viceversa.

Poiché l'equazione caratteristica  di JC ha comunque coefficienti reali, gli autovalori sono reali o accoppiati in complessi coniugati; perciò o formano coppie 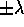reali, oppure coppie immaginarie pure 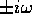, oppure quaterne complesse 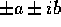. Il solo caso in cui il punto di equilibrio del sistema linearizzato può essere stabile è quello in cui gli autovalori sono tutti immaginari puri; questa però è una condizione necessaria ma non sufficiente per la stabilità del punto di equilibrio.

Si possono classificare i sistemi linearizzati di sistemi hamiltoniani usando la forma canonica di Jordan reale  della matrice JC del linearizzato; si veda [Arnold 86], Appendice 6.

Teorema di stabilità del minimo :  Se il punto stazionario 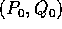della hamiltoniana H(P,Q) è un punto di minimo locale forte , allora è un punto di equilibrio stabile .

Dimostrazione:

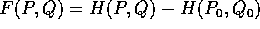La funzione è una funzione di Lyapounov  per il punto di equilibrio 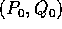, per cui basta applicare il teorema di stabilità di Lyapounov .

 C.D.D.

Usando la stessa funzione F(P,Q) usata in questa dimostrazione, si mostra che un punto di equilibrio di un sistema hamiltoniano non può essere in nessun caso asintoticamente stabile; infatti, poiché 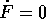, il valore di F(P(t),Q(t)) non può avere per limite 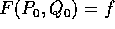, come accade per le orbite del bacino di attrazione, a meno che non sia uguale al valore f sin dalla condizione iniziale.

Per il teorema di esistenza delle curve eccezionali  in dimensione 2, e per i teoremi analoghi in dimensione superiore, si può dimostrare che ogni volta che JC ha un esponente di Lyapounov , non solo il sistema linearizzato, ma anche il sistema nonlineare di Hamilton ha un punto di equilibrio instabile .

Restano però due problemi aperti, nel senso che la risposta non è stata trovata neppure dalla ricerca matematica recente:

(I)

Se un punto di equilibrio non è un minimo locale della hamiltoniana, allora è necessariamente instabile? Questo è stato dimostrato soltanto nel caso di un grado di libertà.

(II)

Se un punto di equilibrio è linearmente stabile  , nel senso che tutti gli autovalori del sistema linearizzato sono immaginari puri e distinti, allora è stabile? Si conoscono dei controesempi, quindi per assicurare la stabilità occorrono delle ipotesi aggiuntive, che però non sono note.

Linearizzazione di sistemi newtoniani

Consideriamo un sistema conservativo del tipo che proviene da un sistema newtoniano ; usando la formulazione lagrangiana, la funzione lagrangiana  sarà del tipo

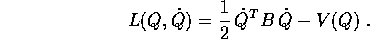
dove B=B(Q) è una matrice definita positiva (quindi invertibile) di tipo 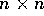; le equazioni di Lagrange sono:

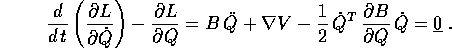
Per mettere in evidenza i punti di equilibrio, riscriviamo le equazioni di Lagrange come sistema dinamico in :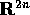

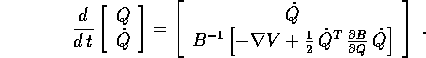
Il secondo membro si annulla solo per 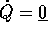e per quei 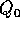tali che .

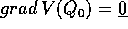Il corrispondente sistema linearizzato in 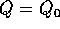è

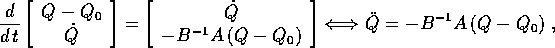
dove la matrice B si intende calcolata in 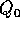, ed 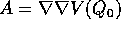è la hessiana di V(Q) calcolata in 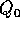; supponiamo che V(Q) sia di classe 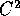, in modo che A sia simmetrica. Il sistema linearizzato è a sua volta lagrangiano, con lagrangiana  quadratica

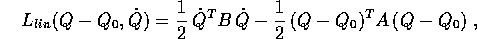
che coincide con il polinomio di Taylor di ordine due (nel punto 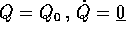) della lagrangiana completa.

Ci poniamo il problema di semplificare il sistema linearizzato, ricorrendo ad un cambiamento di coordinate. Poiché le matrici 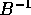ed A sono simmetriche, e 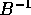e definita positiva, per il teorema di diagonalizzazione simultanea  esiste una matrice invertibile R che le diagonalizza entrambe, quindi diagonalizza il loro prodotto:

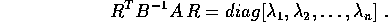
Trasformando direttamente le equazioni di Lagrange (nella forma risolta rispetto alle derivate seconde) con il cambiamento di coordinate , si ottiene

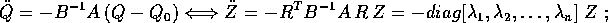
allora nelle coordinate 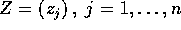le equazioni di Lagrange diventano

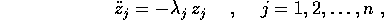
che corrispondono ad un sistema di oscillatori lineari disaccoppiati, studiabili indipendentemente l'uno dall'altro. Se, per un certo j, 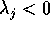, allora 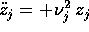è un oscillatore lineare corrispondente a una sella , con soluzioni esprimibili in termini di esponenziali, con esponenti (dove 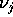è l'esponente di Lyapounov ) con costanti di integrazione 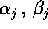. Il sistema linearizzato non è stabile (e neppure quello nonlineare); tuttavia il sistema linearizzato è ``integrabile'', nel senso che si possono scrivere le soluzioni, anche se non formano varietà invarianti compatte.

Oscillazioni proprie

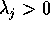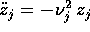Se, per un certo j, si ha , allora è un oscillatore armonico , quindi le soluzioni contengono funzioni trigonometriche nella frequenza propria  :

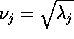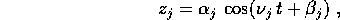
con costanti di integrazione 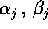che si possono calcolare in funzione della condizione iniziale. Ciascuna di queste soluzioni è un'oscillazione propria  , che si svolge nel piano delle fasi indipendentemente dalle altre. La soluzione nelle coordinate sarà esprimibile come una combinazione lineare di oscillazioni proprie:

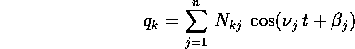
dove i coefficienti 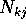dipendono dalle costanti di integr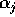azione e dalla matrice di rotazione R. In altre parole nelle variabili Q le oscillazioni sono accoppiate, ma la forma più semplice è ottenibile passando alle variabili ``proprie'', legate alla diagonalizzazione dell'equazione.

Se tutti gli autovalori sono positivi, cioè se il punto 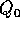è un minimo locale non degenere per l'energia potenziale V, allora il sistema si riduce ad un prodotto diretto di oscillatori armonici. Questo caso rientra nel teorema di Arnold-Jost , poiché le costanti di integrazione 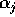sono integrali primi in commutazione , e ogni insieme di livello con le costanti 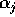tutte >0 è un toro, sul quale il moto è un flusso di Kronecker  avente come frequenze le frequenze proprie 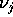. Naturalmente, nel caso di un sistema linearizzato si possono scrivere direttamente le soluzioni senza passare attraverso le complicazioni della dimostrazione del teorema di Arnold-Jost.

 
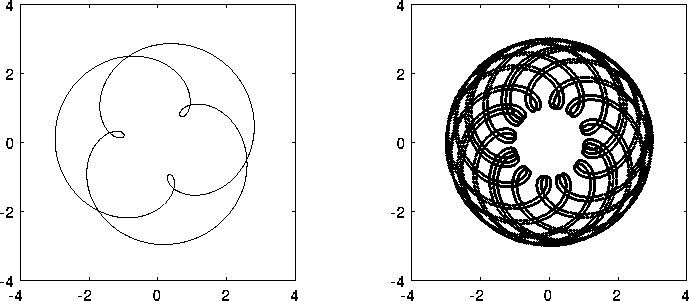
Figure 7.12:  A sinistra, figura di Lissajous con rapporto di frequenze 5/2; a destra, il rapporto delle frequenze è irrazionale (exp(1)) e la curva non si ripete mai; alla lunga ``riempirebbe'' la corona circolare.

Nello spazio delle variabili originarie, in cui le oscillazioni sono accoppiate, le soluzioni disegnano delle traiettorie complicate, la cui forma dipende dai rapporti tra le frequenze proprie. Per esempio per n=2 nel piano delle variabili 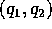le traiettorie sono delle figure di Lissajous   (Figura 7.12), che sono curve chiuse (ma non semplici) se 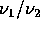è razionale. Per rapporti di frequenze irrazionali, la traiettoria passa ``dappertutto'', in un senso che è precisato dal seguente teorema.

Teorema del ritorno :  Dato un flusso di Kronecker  sul toro bidimensionale 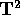, con coordinate angolo :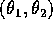

con rapporto delle frequenze 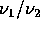irrazionale, allora ogni orbita passa arbitrariamente vicina ad ogni punto del toro.

Dimostrazione:

Fissiamo un passo temporale h e consideriamo il flusso per un tempo h



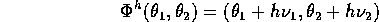
come una trasformazione 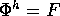del toro in sé, che conserva l'area; perciò dato un intorno D arbitrariamente piccolo del punto iniziale 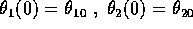, le immagini 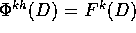hanno tutte la stessa area Area(D). Allora esiste un intero k>0 tale che 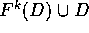non è vuoto, altrimenti l'unione disgiunta degli 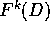per ogni k avrebbe area più grande di 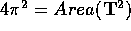. Poiché il flusso integrale è continuo, e l'orbita per 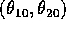non è periodica, ne segue che l'orbita ripassa arbitrariamente vicina alla condizione iniziale per un certo t=kh>0.

Scegliendo h in modo che 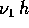sia in rapporto irrazionale con 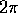, il punto di ritorno ha la coordinata 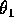diversa da quella iniziale, ma arbitrariamente vicina ad essa, diciamo 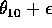. Allora per tempi t=mkh, con m intero, l'orbita passa da 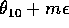, quindi passa infinite volte da valori principali che distano meno di da un qualunque valore in 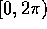. Se anche 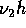è in rapporto irrazionale con 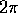, lo stesso si verifica sull'asse 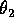, e poiché in ogni intervallo dei valori principali di 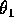si trovano infiniti punti della forma 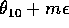, tra questi ce ne saranno in ogni intervallo di ampiezza dei valori principali di .

 C.D.D.

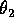Il teorema precedente si applica quindi ad ogni sistema hamiltoniano integrabile  a due gradi di libertà; in effetti lo stesso teorema vale anche per un numero qualsiasi di gradi di libertà. Nel caso dei sistemi linearizzati con due gradi di libertà, se ci sono due frequenze proprie 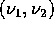in rapporto irrazionale, allora i valori principali delle fasi delle oscillazioni passano arbitrariamente vicino ad ogni punto del quadrato 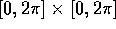, e quindi le variabili proprie 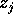passano arbitrariamente vicino ad ogni punto della corona circolare

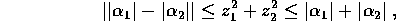
come si vede in Figura 7.12.

Esempio:

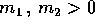Riprendiamo il pendolo doppio  con masse , la prima a distanza da un punto fisso e la seconda a distanza L>0 dalla prima; supponiamo che esista un'energia potenziale la cui espressione, nelle coordinate cartesiane 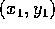ed 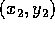dei due corpi, sia 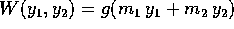, con g>0.

Usiamo come coordinate lagrangiane le due variabili angolo 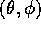che esprimono l'angolo tra la verticale (asse delle y negative) e le aste di ciascuno dei due pendoli; allora, come già calcolato nella Sezione 6.3, la lagrangiana  è:



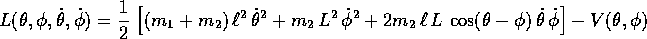
con energia potenziale



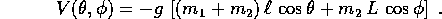
I punti stazionari di V, che soddisfano 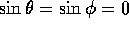, fornisvono quattro punti di equilibrio distinti: 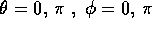. Il minimo è ovviamente quello corrispondente alla configurazione con i due pendoli verso il basso: calcolando la parte quadratica della lagrangiana in 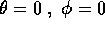si ricava



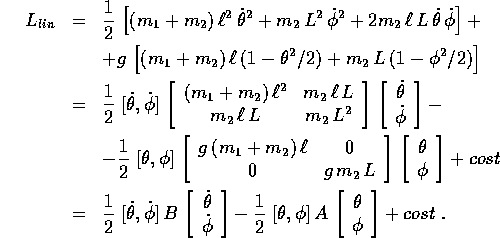
Indicando con 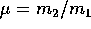il rapporto tra le due masse, la soluzione del problema linearizzato si ottiene trovando gli autovalori della matrice diagonalizzabile



che ha determinante e traccia maggiori di zero (come già noto, trattandosi di un minimo). Le radici quadrate degli autovalori forniscono le frequenze proprie. Si noti però che le oscillazioni dei due pendoli sono accoppiate, poiché la matrice 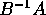non è diagonale: non è perciò possibile mettere in oscillazione uno dei due pendoli, senza che l'oscillazione si propaghi all'altro. Per esempio, se i due pendoli sono uguali: 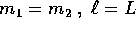, allora



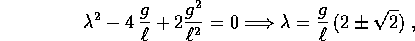
dove sarebbe la frequenza di uno solo di questi pendoli.

Negli altri punti di equilibrio l'energia potenziale, e quindi anche l'energia totale (e la hamiltoniana) non ha dei minimi locali. La linearizzazione si esegue nello stesso modo: cambiano solo alcuni segni (sia in B che in A), e la presenza di uno o due autovalori negativi di 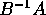giustifica l'instabilità dei punti di equilibrio.

Abbiamo già notato che le coordinate lagrangiane 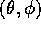non parametrizzano in modo regolare il toro delle configurazioni, precisamente nei punti in cui 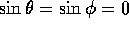. Poiché però queste singolarità del sistema di coordinate sono singolarità isolate , le conclusioni che abbiamo tratte dai calcoli svolti in queste coordinate sono legittime.

Problema Consideriamo due pendoli semplici, della stessa lunghezza 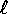e con la stessa massa m, accoppiati da una molla. Nell'approssimazione lineare la lagrangiana, in funzione degli angoli 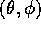dei due pendoli rispetto alla verticale, sarà:

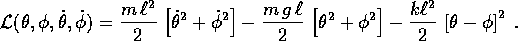
Calcolare esplicitamente la soluzione con condizioni iniziali

(Soluzione)